1 可視化の重要性

データの可視化（≒作図）はデータ分析において不可欠である。むしろ、統計的分析より重要なこともしばしばである。「言うほど重要か？」と思う人がいるかもしれないので、有名な「アンスコムの例（Anscombe’s quartet）」を使ってそれを例証してみよう。

1.1 アンスコムの例

仮に4人の学生が同じ実験を実施したとする（それぞれ実験I, II, III, IV）。その実験では参加者（各11名）の個人傾向を様々な尺度で測定しており、ここでは変数「x」と「y」が測定されたと考えてみてほしい（変数は別に「x」と「y」である必要はなく、「身長」と「体重」などでも良い）。

4人はそれぞれの実験における変数xとyの平均値（mean; M）と標準偏差（standard deviation; SD）と相関係数（correlation coefficient; r）を計算し、ゼミで報告した（下の表は適当に解読してほしい）。

experiment mean_x sd_x mean_y sd_y pearson_r
I 9 3.316625 7.500909 2.031568 0.8164205
II 9 3.316625 7.500909 2.031657 0.8162365
III 9 3.316625 7.500000 2.030424 0.8162867
IV 9 3.316625 7.500909 2.030579 0.8165214


この表からわかるように、どの実験でもxとyの平均値、標準偏差、相関係数はほとんど同じだった。

……

という報告を私たちはついついやりがちである。しかし、これらの報告はデータの重要な性質を見落としている。

では、ここでxとyの散布図を描いてみよう。

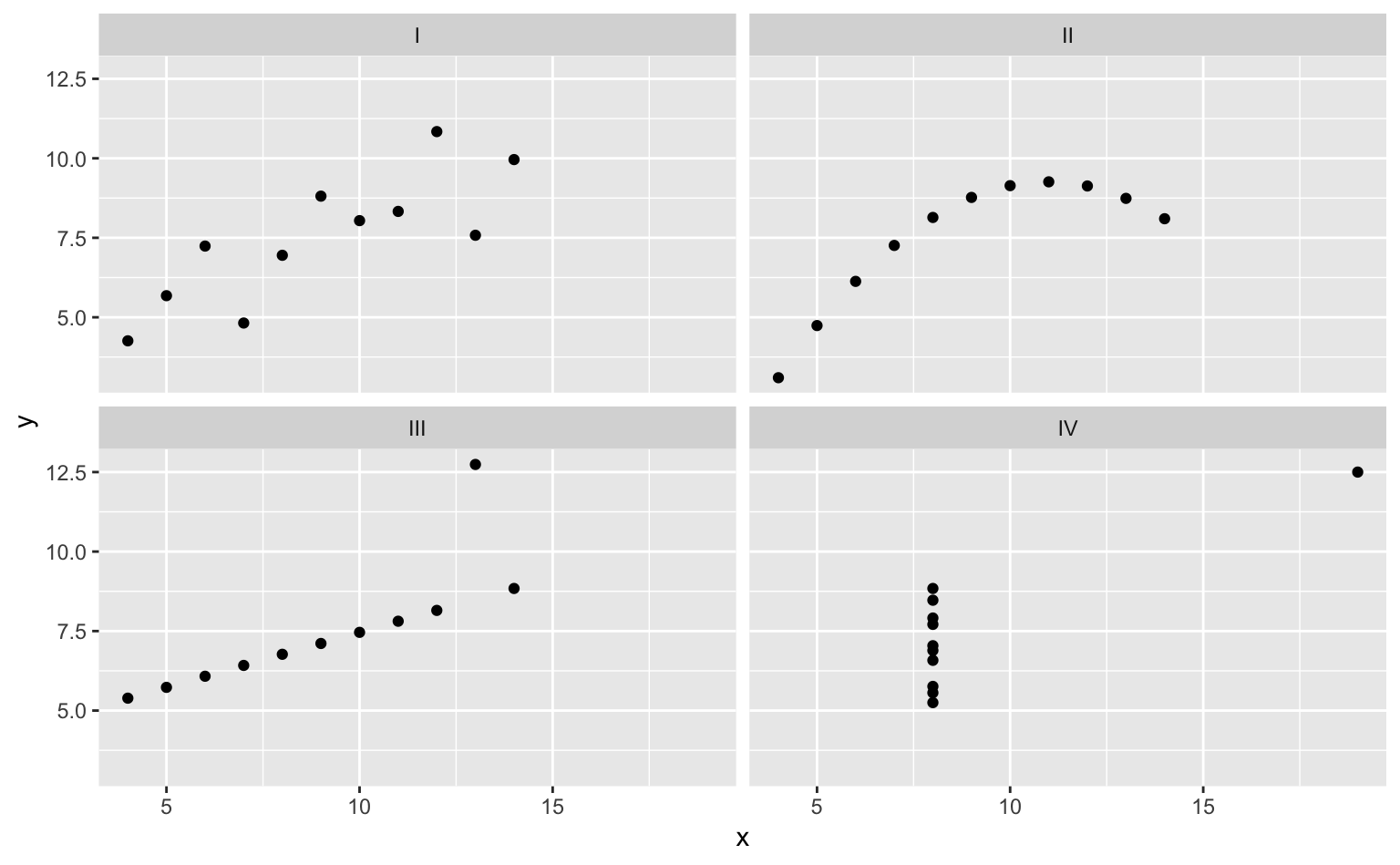
「アンスコムの例」の散布図。どの変数も統計量（平均値、標準偏差、相関係数）の上では同じだが、実際は明らかに異なるパターンを示していることがひと目でわかる。

Figure 1.1: 「アンスコムの例」の散布図。どの変数も統計量（平均値、標準偏差、相関係数）の上では同じだが、実際は明らかに異なるパターンを示していることがひと目でわかる。

上の図を見てひと目でわかるように、xとyの平均値、標準偏差、相関係数が同じであるにもかかわらず、各実験のデータは全く異なる様相を呈していた。

このように、可視化は非常に強力なデータ分析手法の一つである（スプレッドシートの数字だけを見て、これらの図を頭に思い浮かべられる人はいるだろうか？）。また、この例は可視化の本質を私たちに教えてくれる。その本質とは、


  • 変数の数量や分布（distribution）がひと目で分かる

  • 変数間の関係（association）がひと目でわかる


ということである。少し乱暴にまとめてしまうと、グラフとは変数の分布や関係を可視化したものにほかならない。

「ひと目でわかる」という点も重要である。もし発表者が表や統計量だけを見せ、それをもとに議論を始めたら、あなたはどのように感じるだろうか？　数字ばかり見せられた聴衆は話をフォローできなくなるし、そもそも最初から聞く耳を持たなくなってしまう場合もある。ヒトの認知資源には限りがあるし、わかりにくい話にずっと耳を貸していられるほど人々は親切でもないと思っておいたほうが賢明だろう。

とにかく、まずは黙って「可視化からはじめよ」を肝に銘じてほしい。

1.2 可視化のツール：ggplot2

さて、データ分析＋論文用の可視化にはRという統計ソフトのggplot2というパッケージ（tidyverseというパッケージ群の1つ）が便利である。逆に言えば、tidyverseやggplot2がなければRを使うメリットは見いだせないと言っても過言ではない。

ggplot2がなぜ便利なのかを一言で説明するのは難しいが、なぜ他のツールーーたとえばEx○elーーが不便なのかはすぐに列挙できる。

  • 作図が面倒

  • 美しくない（ugly!）

  • 再現性に欠ける（グラフの縦横比、色、コピペ汚染）

……などなど。他にもあるかもしれない。

しかし、あまり悪口ばかり書いても仕方がないので、早速Rとggplot2を使ってみることにしよう。