4 分布

Chapter 1の「アンスコムの例」で見たように、データの要約統計量（summary statistics；記述統計量、descriptive statisticsとも言う）だけに注目して、分布（distribution）を確認しないと痛い目にあうことがある。

実験や調査でデータを集めたら、要約統計量を計算するだけでなく、まずデータの分布を確認・報告することを心がけよう。

library(ggplot2) # 忘れずにパッケージを読み込む

4.1 ヒストグラム

4.1.1 基本のヒストグラム

分布を表すグラフの中で最も代表的なのはヒストグラム（histogram）だろう。ヒストグラムは複数の縦棒から構成されるグラフで、棒の幅（x軸）は変数の値、棒の高さ（y軸）はデータの個数を表している。

早速具体例を見てみよう。Chapter 1と同様に、ここでもgcookbookのtophitters2001（2001年MLBにおける144名の打手データ）を使うことにする。gcookbookを読み込み、改めてデータ構造を再確認しよう。

library(gcookbook)

head(tophitters2001) # データの先頭6行を再確認

##          id   first   last           name year stint team lg   g  ab   r
## 1 walkela01   Larry Walker   Larry Walker 2001     1  COL NL 142 497 107
## 2 suzukic01  Ichiro Suzuki  Ichiro Suzuki 2001     1  SEA AL 157 692 127
## 3 giambja01   Jason Giambi   Jason Giambi 2001     1  OAK AL 154 520 109
## 4 alomaro01 Roberto Alomar Roberto Alomar 2001     1  CLE AL 157 575 113
## 5 heltoto01    Todd Helton    Todd Helton 2001     1  COL NL 159 587 132
## 6  aloumo01  Moises   Alou    Moises Alou 2001     1  HOU NL 136 513  79
##     h 2b 3b hr rbi sb cs  bb  so ibb hbp sh sf gidp    avg
## 1 174 35  3 38 123 14  5  82 103   6  14  0  8    9 0.3501
## 2 242 34  8  8  69 56 14  30  53  10   8  4  4    3 0.3497
## 3 178 47  2 38 120  2  0 129  83  24  13  0  9   17 0.3423
## 4 193 34 12 20 100 30  6  80  71   5   4  9  9    9 0.3357
## 5 197 54  2 49 146  7  5  98 104  15   5  1  5   14 0.3356
## 6 170 31  1 27 108  5  1  57  57  14   3  0  8   18 0.3314

では、144名の打手の打率（avg）の分布を可視化してみよう。ヒストグラムはx軸に連続変数の値を取るグラフなので、以下のようにコードを書けば良い。

ggplot(tophitters2001, aes(avg)) + # x軸にavg；データの個数は自動的にカウントされるので、yは指定する必要なし
  geom_histogram() # ヒストグラムを描く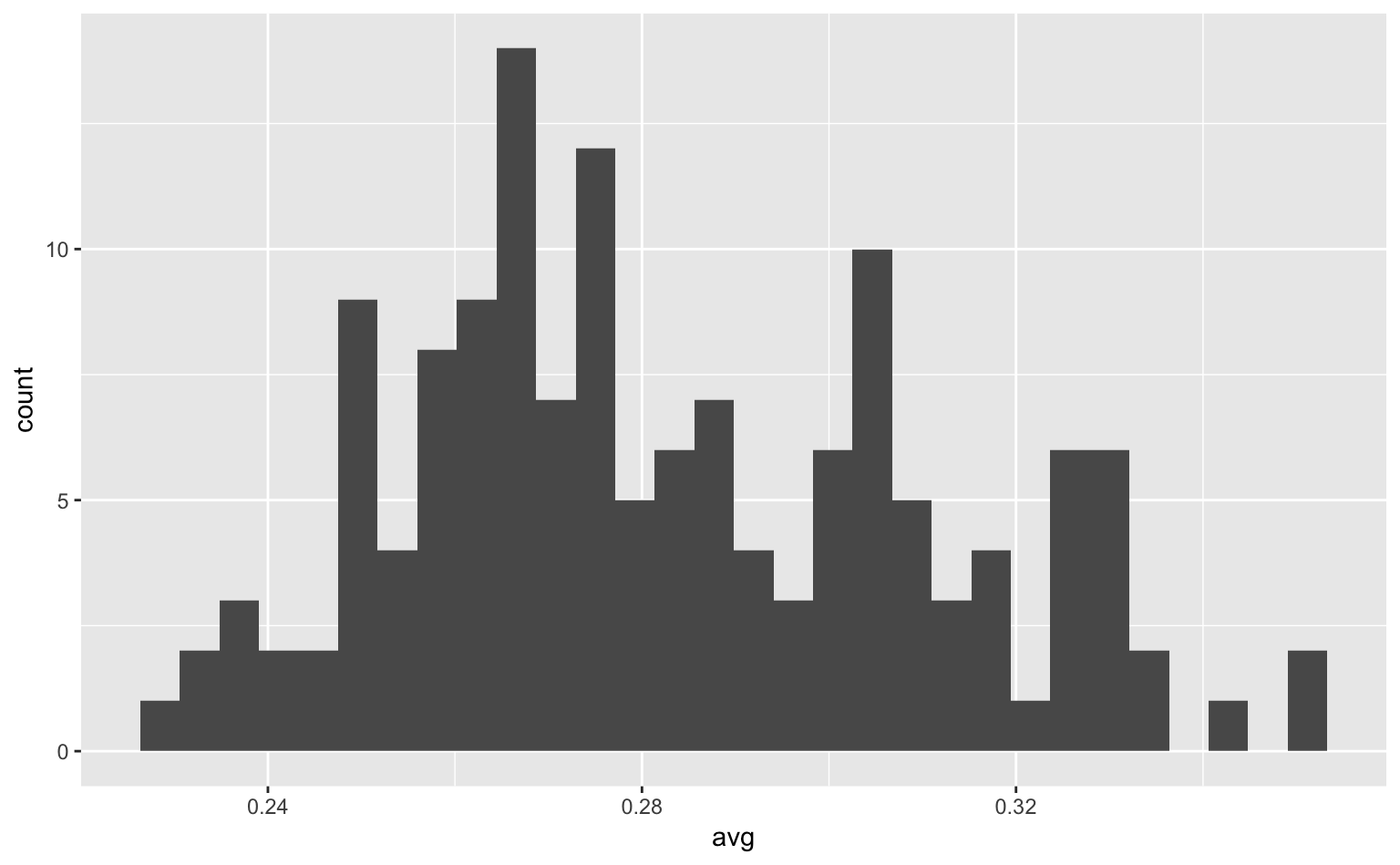

Figure 4.1: 2001年MLBにおける144名の打率の分布。

グラフを見ると、大体0.28前後が中央値（median）あるいは最頻値（mode）になっていることがわかる。

なお、ビン（bin：ヒストグラムの1本1本の棒）の幅を調整することで、分布の印象が大幅に変わるということに注意してほしい。実際、上のグラフを描いた際に、

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

というメッセージが出たかと思う。これはまさにそのことを注意喚起するメッセージである。

データ分析の際は、ビンの幅をいくつか試した上で、最も妥当そうな値を使うようにすると良い。参考に、ビンの幅をそれぞれ0.001、0.01、0.1にした場合の図を下に載せておく。

ggplot(tophitters2001, aes(avg)) +
  geom_histogram(binwidth = 0.001) # binwidth = ...でビンの幅を設定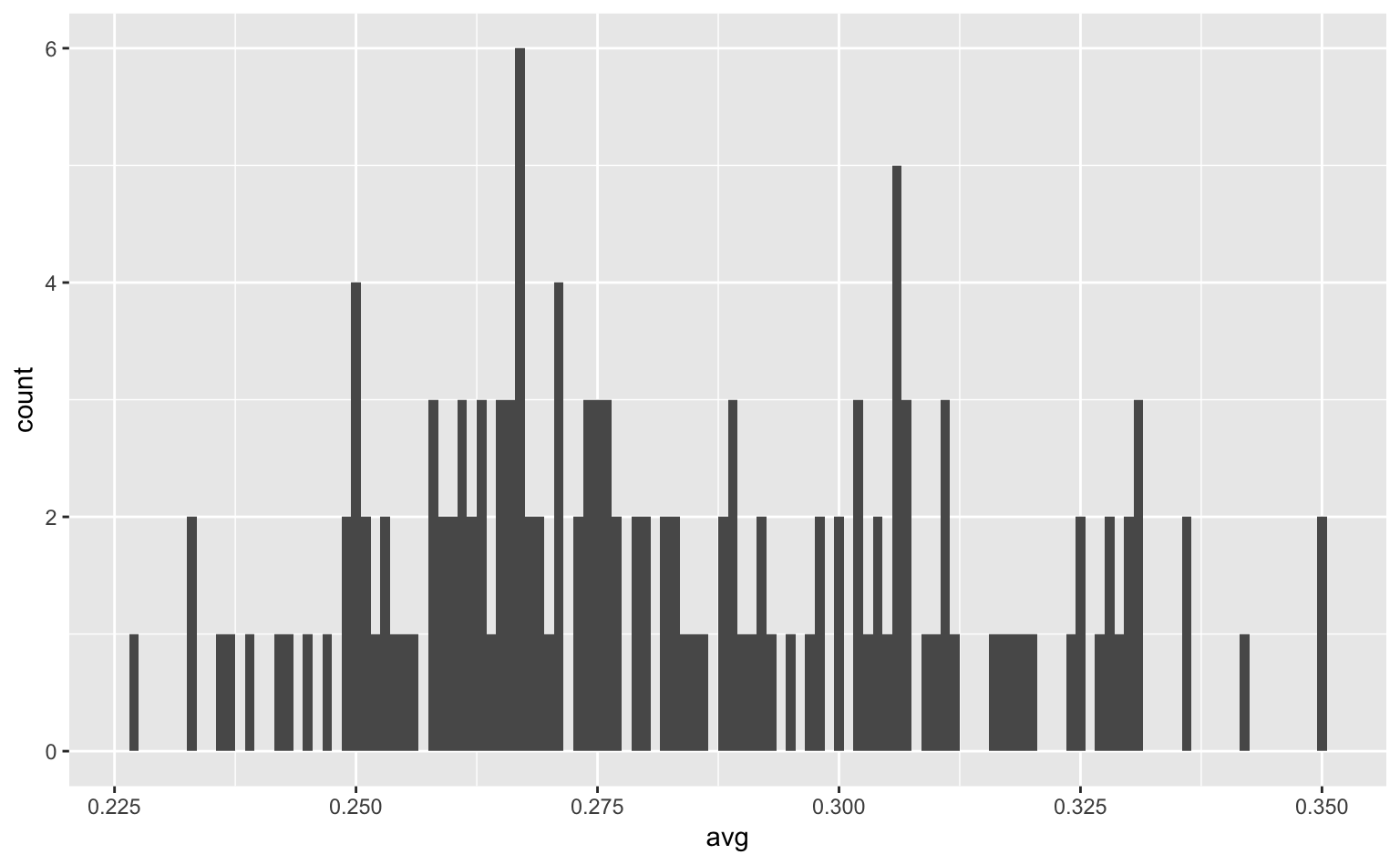

Figure 4.2: ビンが細すぎるヒストグラム。

ggplot(tophitters2001, aes(avg)) +
  geom_histogram(binwidth = 0.01) # binwidth = ...でビンの幅を設定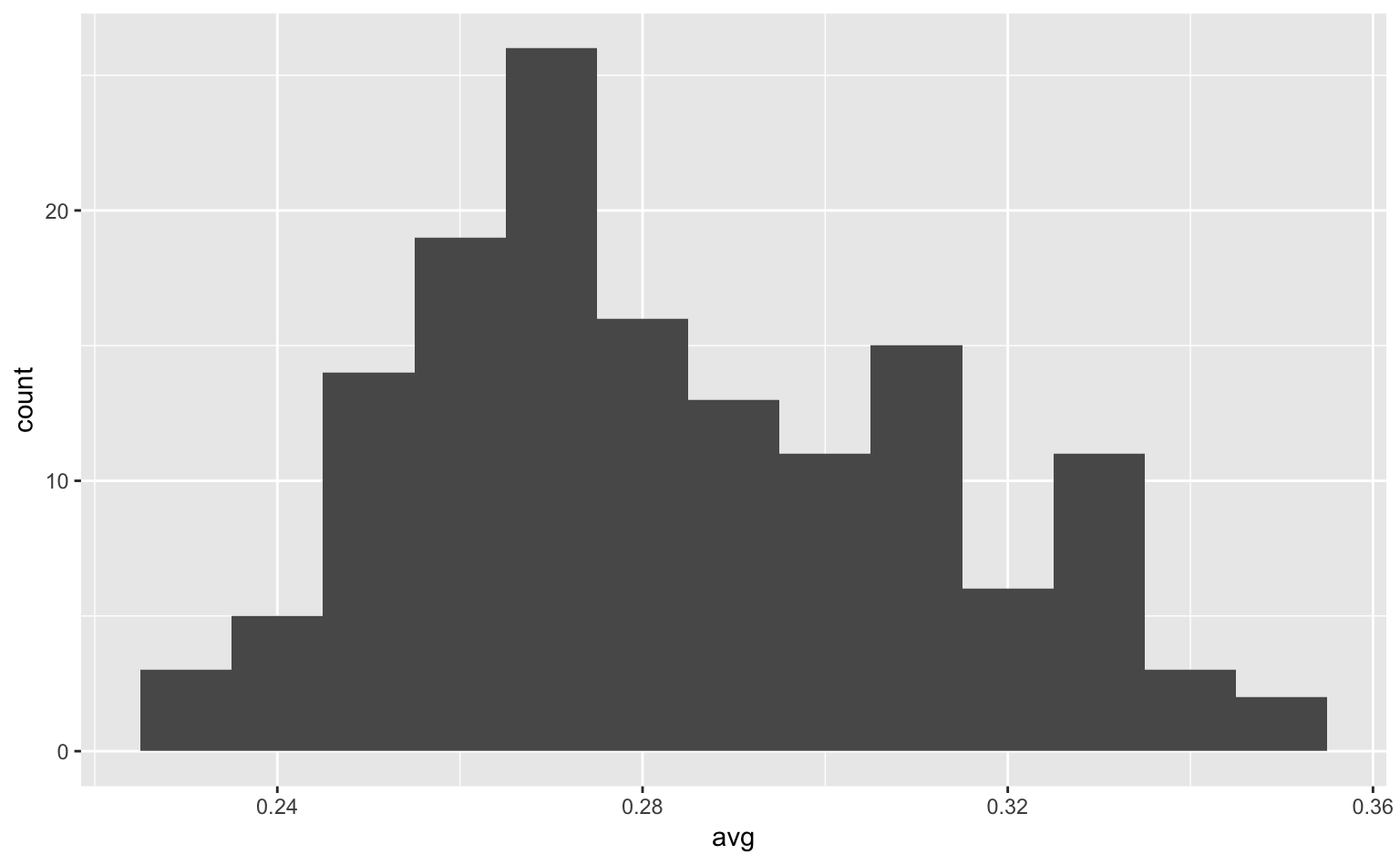

Figure 4.3: ビンが妥当なサイズのヒストグラム。

ggplot(tophitters2001, aes(avg)) +
  geom_histogram(binwidth = 0.1) # binwidth = ...でビンの幅を設定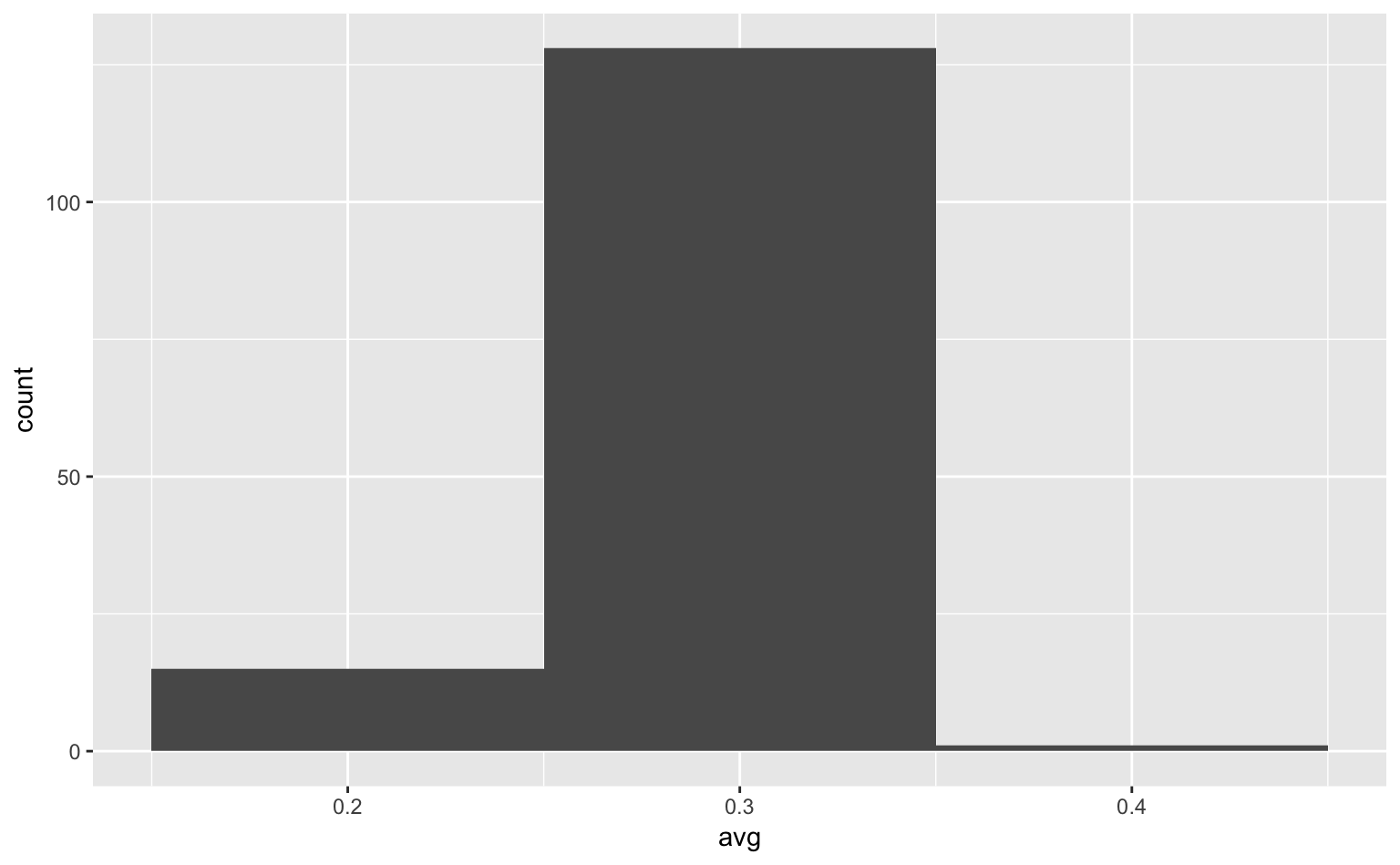

Figure 4.4: ビンが太すぎるヒストグラム。

4.1.2 グルーピングされたヒストグラム

たとえば、実験や調査をおこなった際、変数の分布をある集団ごとに見比べたい（グルーピングしたい）ということがあるかと思う。たとえば、「○○の尺度得点の分布は男女間で異なるのでは？」とか、「実験群と統制群とで○○の分布に違いがあるのでは？」などである。

引き続きtophitters2001を使って、その具体例を見てみよう。ここでは、リーグごとの打率の分布を見比べることにする。

lg：打手の所属リーグ（AL or NL；それぞれア・リーグとナ・リーグ）

このようなときは、fillにグルーピングしたい変数（lg）を指定すれば良い。

ggplot(tophitters2001, aes(avg, fill = lg)) + # x軸にavg；fillに変数を指定することでグルーピングできる
  geom_histogram(position = "identity") # position = "identity"としないといけない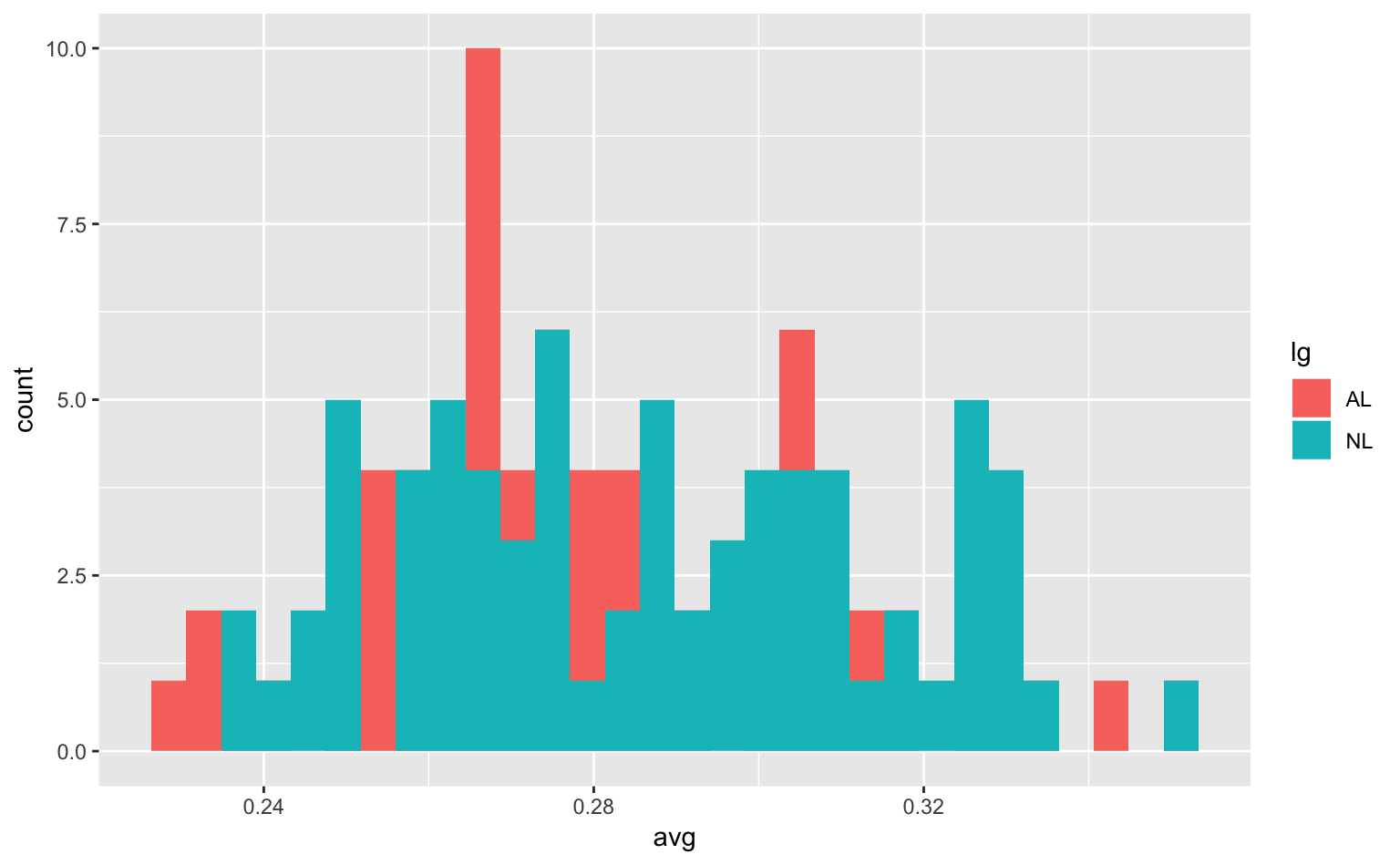

Figure 4.5: リーグごとの打率のヒストグラム。

なお、ここではposition = "identity"と設定しなくてはならない。なぜなら、geom_histogram()はposition = "stack"がデフォルト設定であり、そのままだと積み上げ棒グラフのようになってしまうからである。気になる人は、position = "identity"の部分を消した上で、もう一度グラフを描いてみよう。

また、基本的には上のヒストグラムでも問題ないが、ア・リーグのデータがナ・リーグの後ろに隠れてしまっているのが若干気になる。このようなときは、alphaに0〜1の値を指定すると、ヒストグラムが半透明になり、上の問題を解決できる。

ggplot(tophitters2001, aes(avg, fill = lg)) +
  geom_histogram(position = "identity", alpha = 0.7) # 0だと完全に透明、1だと完全に不透明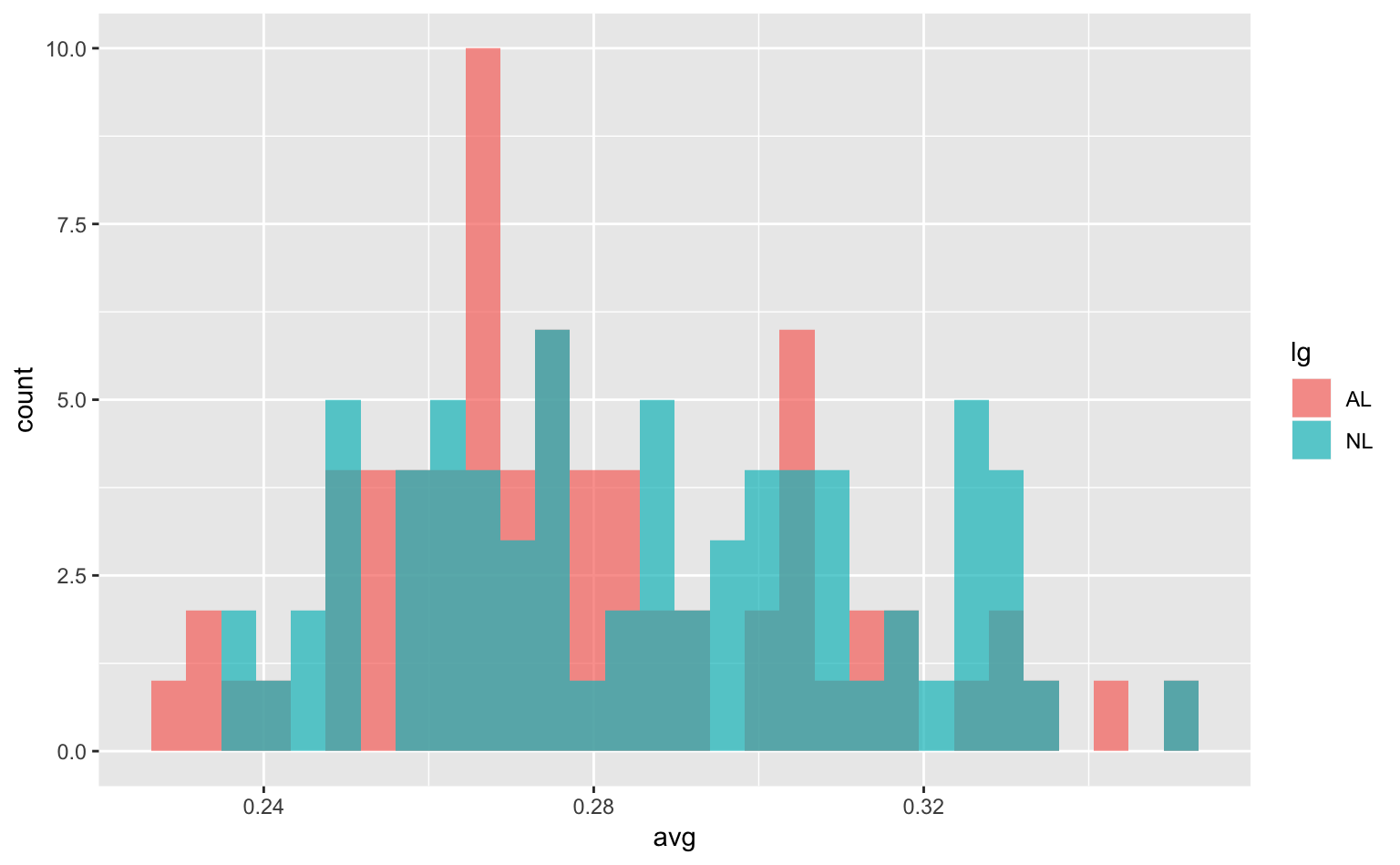

Figure 4.6: Figure 4.5を半透明にしたもの。

無事ア・リーグのデータが見えるようになった。

4.2 密度プロット

ヒストグラムと似たようなグラフに、密度プロット（density plot）がある。密度プロットとは、ヒストグラムのようにローデータ（raw data）をそのままプロットするのではなく、カーネル密度推定（kernel-density estimation）というテクニックで密度分布を推定した上で可視化する手法である。グラフが手書きの時代だった頃からヒストグラムがあるのに対し、密度プロットは計算機の発達によって開発された比較的新しいグラフである。

描き方は簡単で、上でgeom_histogram()としていたところをgeom_density()に差し替えるだけで良い。

ggplot(tophitters2001, aes(avg, fill = lg)) + # x軸にavg；fillに変数を指定することでグルーピングできる
  geom_density(alpha = 0.7) # デフォルトがposition = "identity"なので、geom_histogram(position = "identity")のように明示的に指定する必要がない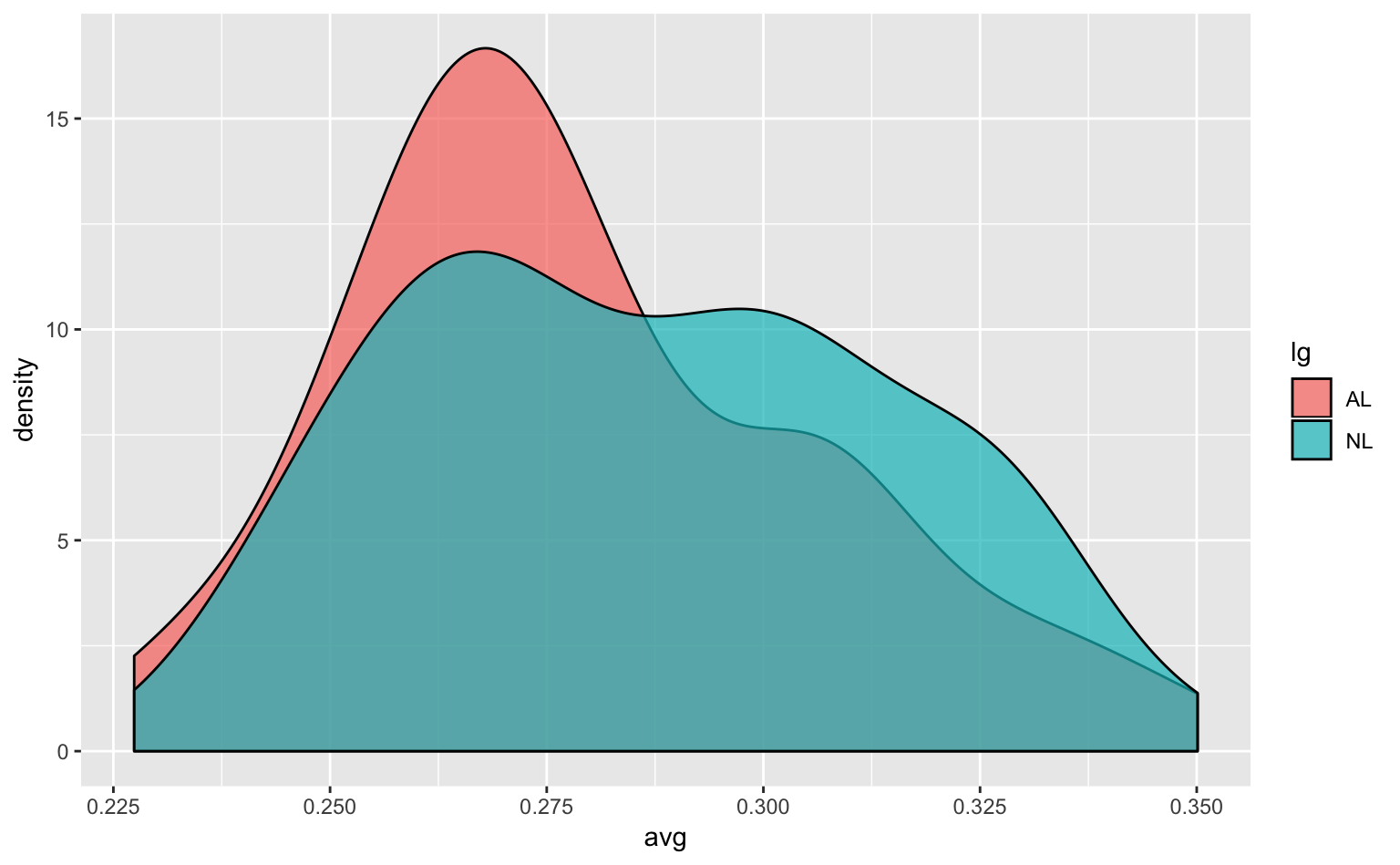

Figure 4.7: リーグごとの打率の密度プロット。

y軸は推定された密度を表している（5人とか10人といった人数を表しているわけではない）。この密度は、塗りつぶされた面積の総和が1になるように算出されているだけなので、値そのものにはあまり意味がないことに注意してほしい。

また、密度プロットもヒストグラムと同様に、描き方次第ではデータの性質を捉えきれないという欠点がある。geom_histogram()ではbinwidthを調整する必要があったが、geom_density()ではadjustという引数（カーネル密度推定に用いられるパラメタ）を調整する必要がある。先程と同様に、adjustの値をそれぞれ0.25, 1, 4にしたグラフを下に載せておく。

ggplot(tophitters2001, aes(avg, fill = lg)) +
  geom_density(alpha = 0.7, adjust = 0.25) # adjust = ...で平滑化の強度を調整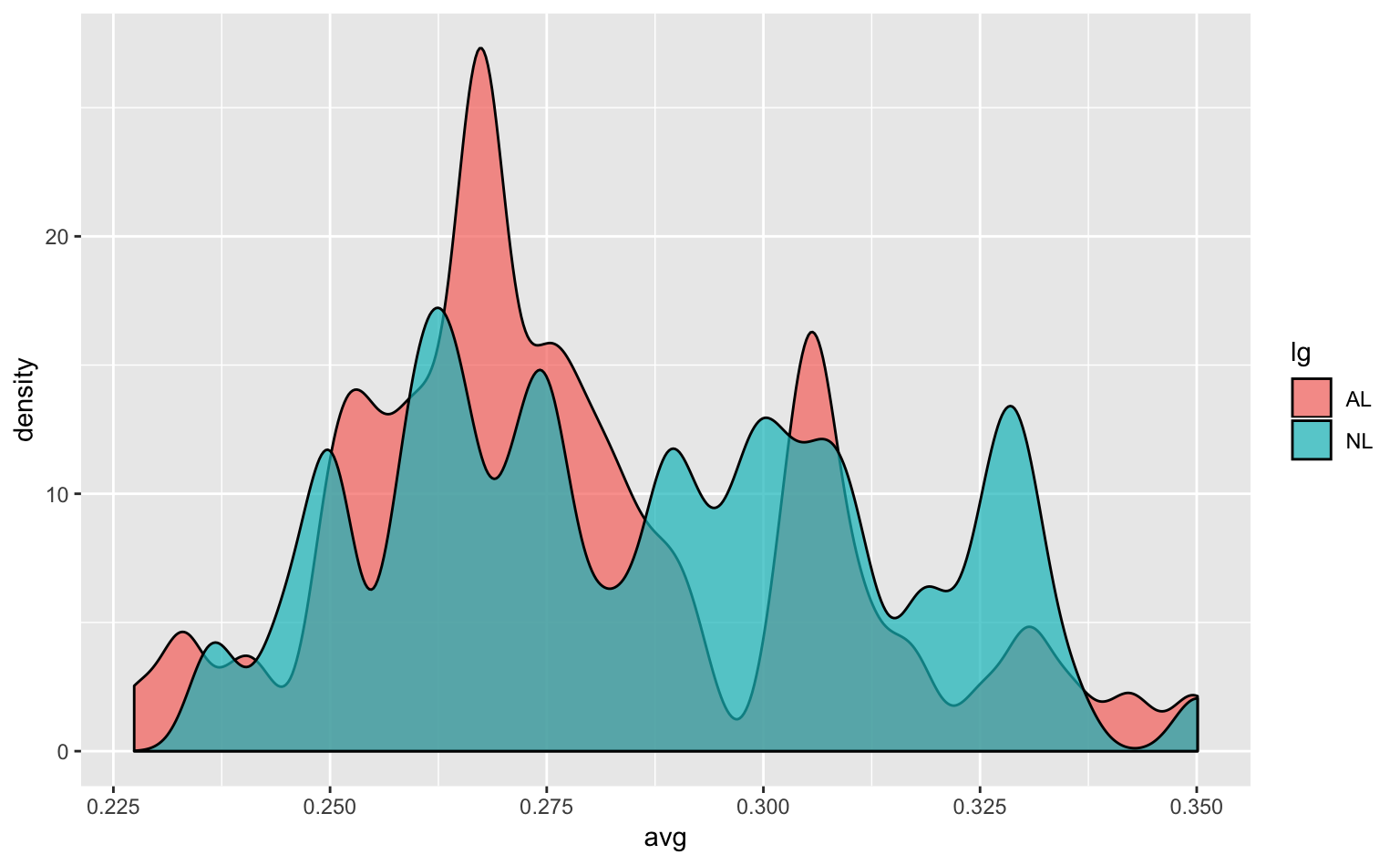

Figure 4.8: 平滑化が弱すぎる密度プロット。データの全体的な特徴が見えにくくなってしまっている。

ggplot(tophitters2001, aes(avg, fill = lg)) +
  geom_density(alpha = 0.7, adjust = 1) # adjust = ...で平滑化の強度を調整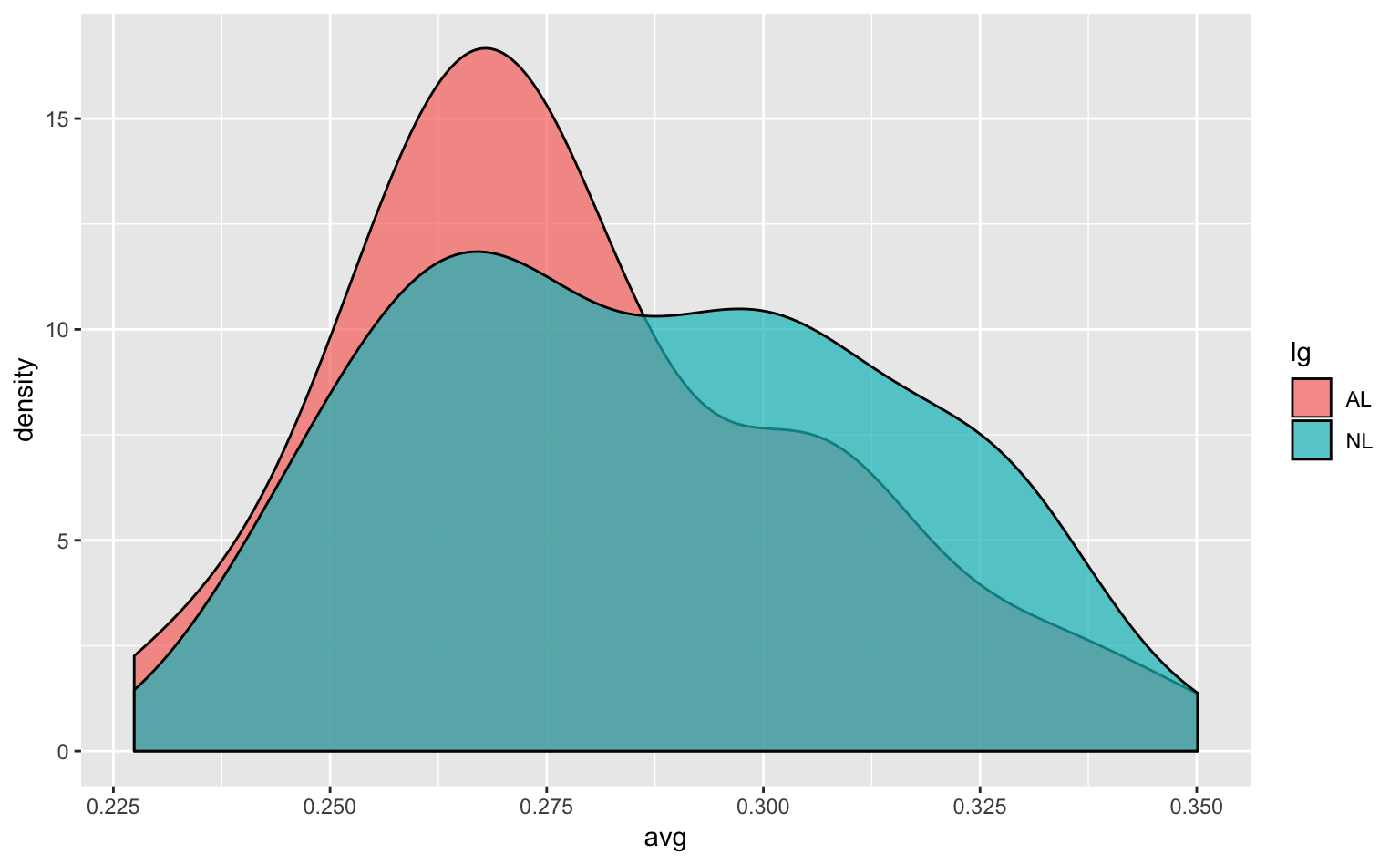

Figure 4.9: 妥当な平滑化の密度プロット（デフォルトの設定）。

ggplot(tophitters2001, aes(avg, fill = lg)) +
  geom_density(alpha = 0.7, adjust = 4) # adjust = ...で平滑化の強度を調整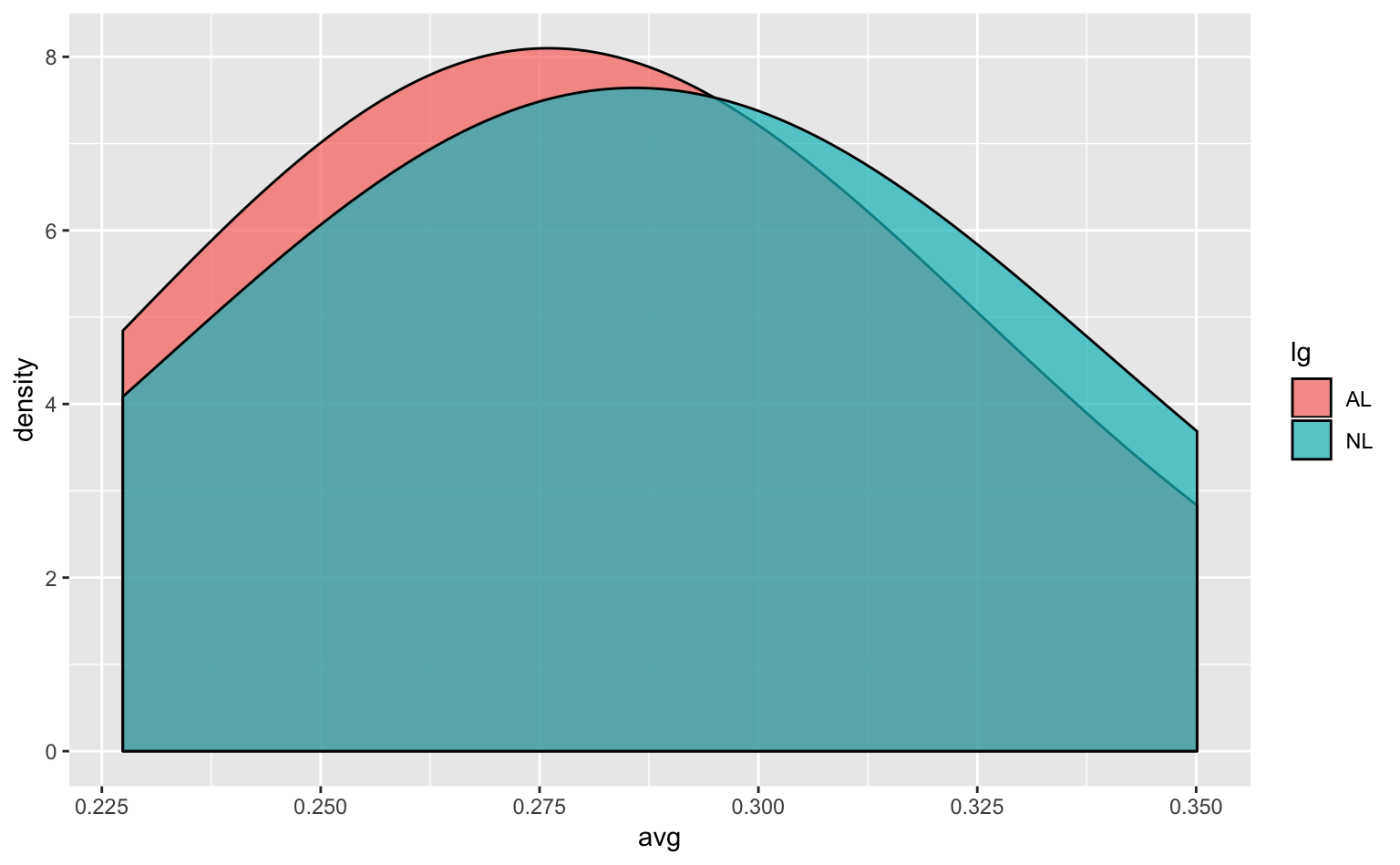

Figure 4.10: 平滑化が強すぎる密度プロット。データを平滑化しすぎており、分布の違いが見えなくなってしまっている。

ところで、Chapter 2でも少し述べたように、ggplot2では複数のプロットを重ね合わせることができる。たとえば、ヒストグラムと密度プロットは以下のように重ね合わせることができる。

ggplot(tophitters2001, aes(avg, y = ..density..)) + # y = ..density..とする必要あり
  geom_histogram(binwidth = 0.01) + # まずヒストグラムを描く
  geom_density(alpha = 0.7) # その上に密度プロットを描く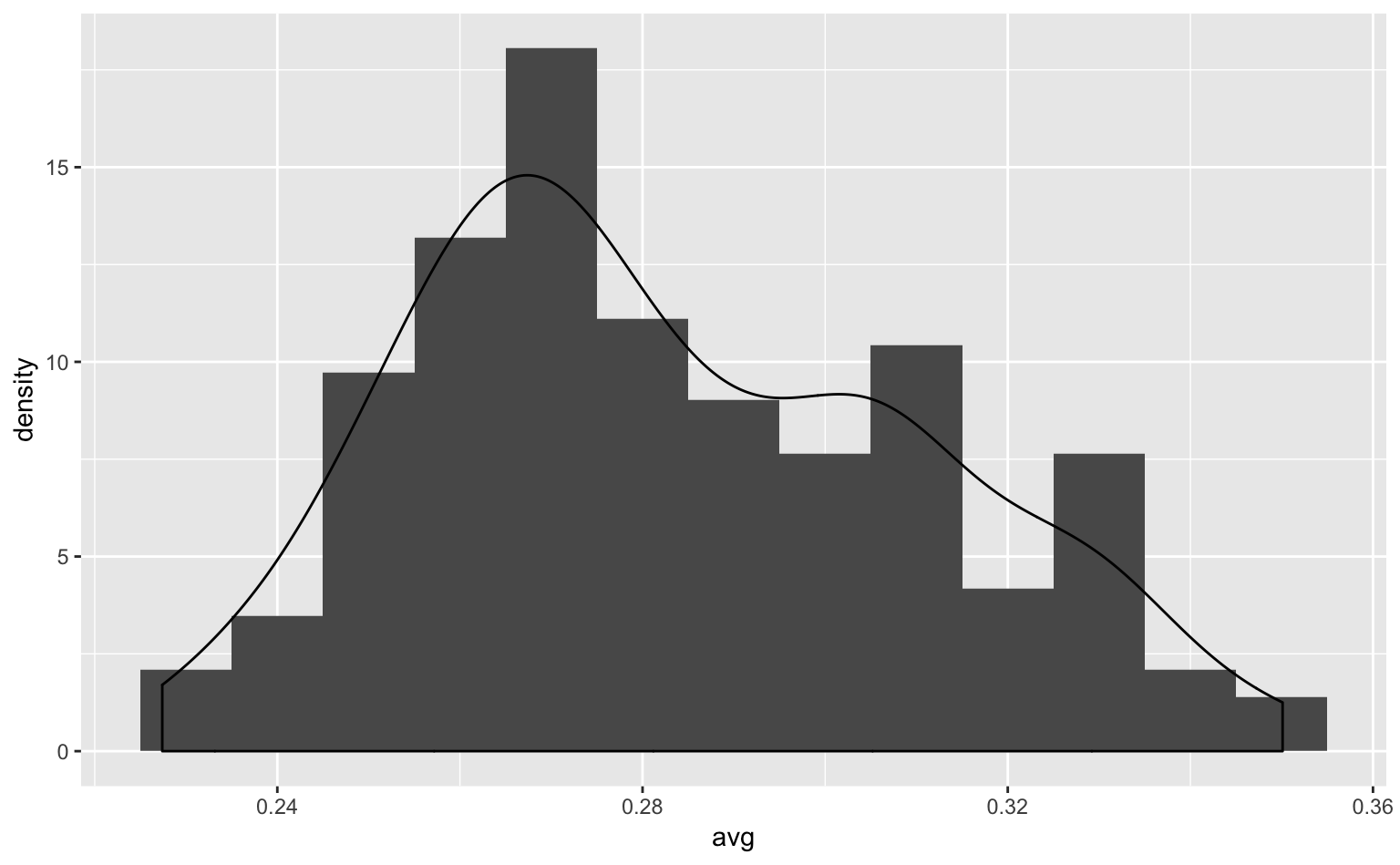

Figure 4.11: ヒストグラムと密度プロットを重ねたグラフ。

なお、ここではy = ..density..をコードに追加する必要がある。なぜなら、geom_density()が密度をy軸に取るのに対し、geom_histogram()はデフォルトでデータの個数をy軸に取ってしまうからである。2つのプロットのy軸の単位を揃えるために、ここでは「データの密度（..density..）をy軸に取ってください」と明示的に指定しなければならない。

4.3 箱ひげ図

ヒストグラムや密度プロットとは異なり、データの要約統計量を示しつつ、同時に分布を表せるようなグラフも存在する。その代表例は箱ひげ図（box plot; box-and-whisker plot）だろう。

ここではRにデフォルトで搭載されているPlantGrowth（植物の重さに関する実験のデータセット）を使うことにする。

head(PlantGrowth) # 先頭6行を確認

##   weight group
## 1   4.17  ctrl
## 2   5.58  ctrl
## 3   5.18  ctrl
## 4   6.11  ctrl
## 5   4.50  ctrl
## 6   4.61  ctrl

このデータには2つの変数があり、それぞれ

group：実験の条件（ctrl, trt1, or trt2）
weight：植物の重さ

を表している。

さて、3つの条件ごとに植物の重さの分布を可視化したい。もちろんヒストグラムや密度プロットでもよいが、ここでは箱ひげ図を使ってみよう。以下のコードで箱ひげ図を描くことができる。なお、箱ひげ図に色をつけるにはfillに変数を指定すれば良い。

ggplot(PlantGrowth, aes(group, weight, fill = group)) + # x軸にgroup、y軸にweight；fillで色の塗りつぶし
  geom_boxplot() # 箱ひげ図を描くためのコード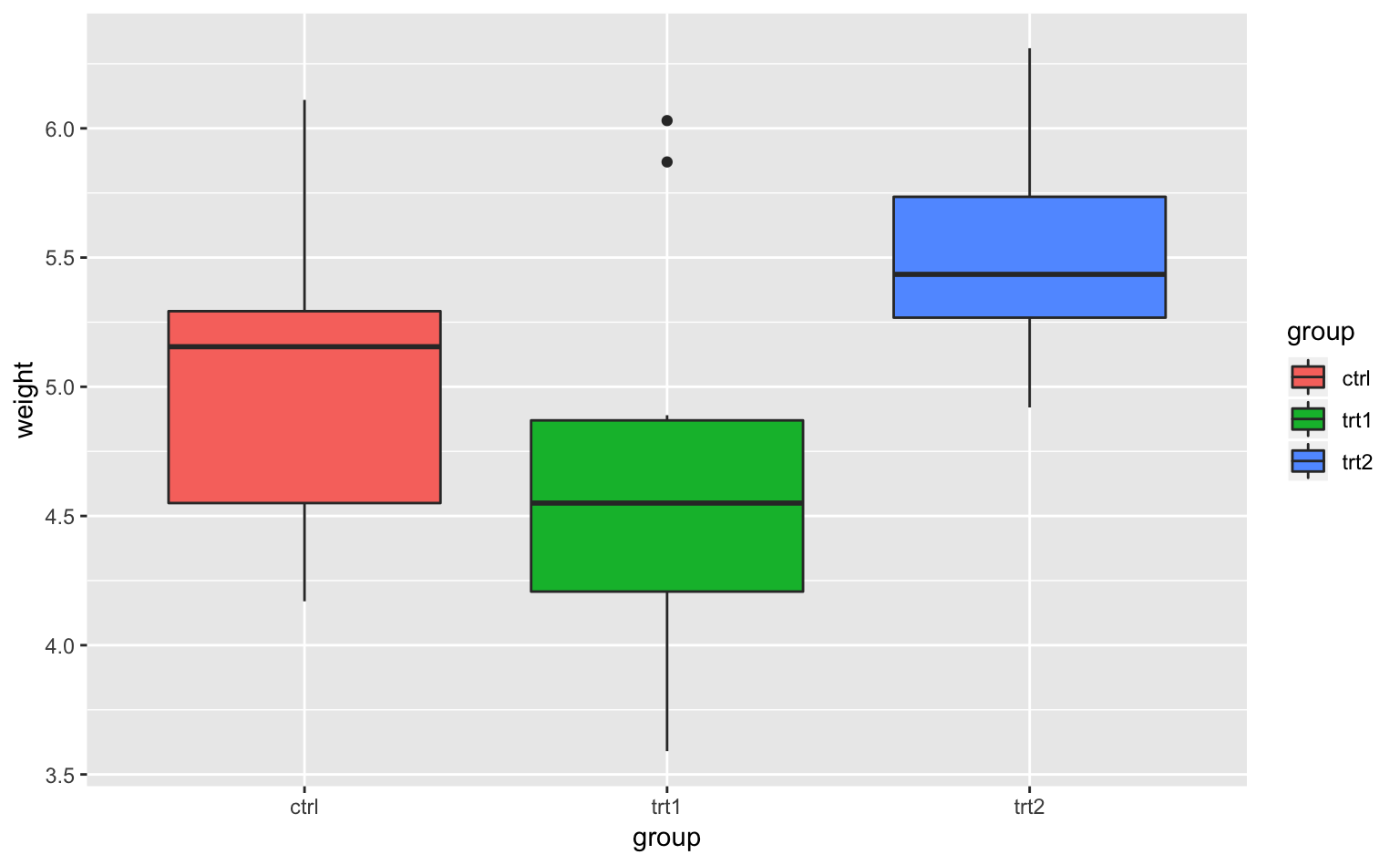

Figure 4.12: 箱ひげ図。x軸は条件、y軸は植物の重さを表している。

何やら謎の図形が現れたが、まさにこれが箱ひげ図である。図形のそれぞれのパーツは以下のものを表している¹¹。

四角（箱）：四分位範囲（interquartile range, IQR）。25パーセンタイルから75パーセンタイルのこと
縦線（ひげ）：四角の上端／下端からIQR × 1.5の範囲
太線：中央値。50パーセンタイル（percentile）とも言う
点：外れ値（outlier；IQR × 1.5より外側の値）

英語版Wikipedia “Interquartile range”（https://en.wikipedia.org/wiki/Interquartile_range）の図が説明としてわかりやすいだろう。

ただし、箱ひげ図だけではデータの平均値を描くことができない¹²。平均値を追加するには、以下のコードを書けば良い。

ggplot(PlantGrowth, aes(group, weight, fill = group)) +
  geom_boxplot() +
  stat_summary(geom = "point", fun.y = mean, color = "white", shape = "diamond", size = 3) # 各引数の意味はなんとなく解読してほしい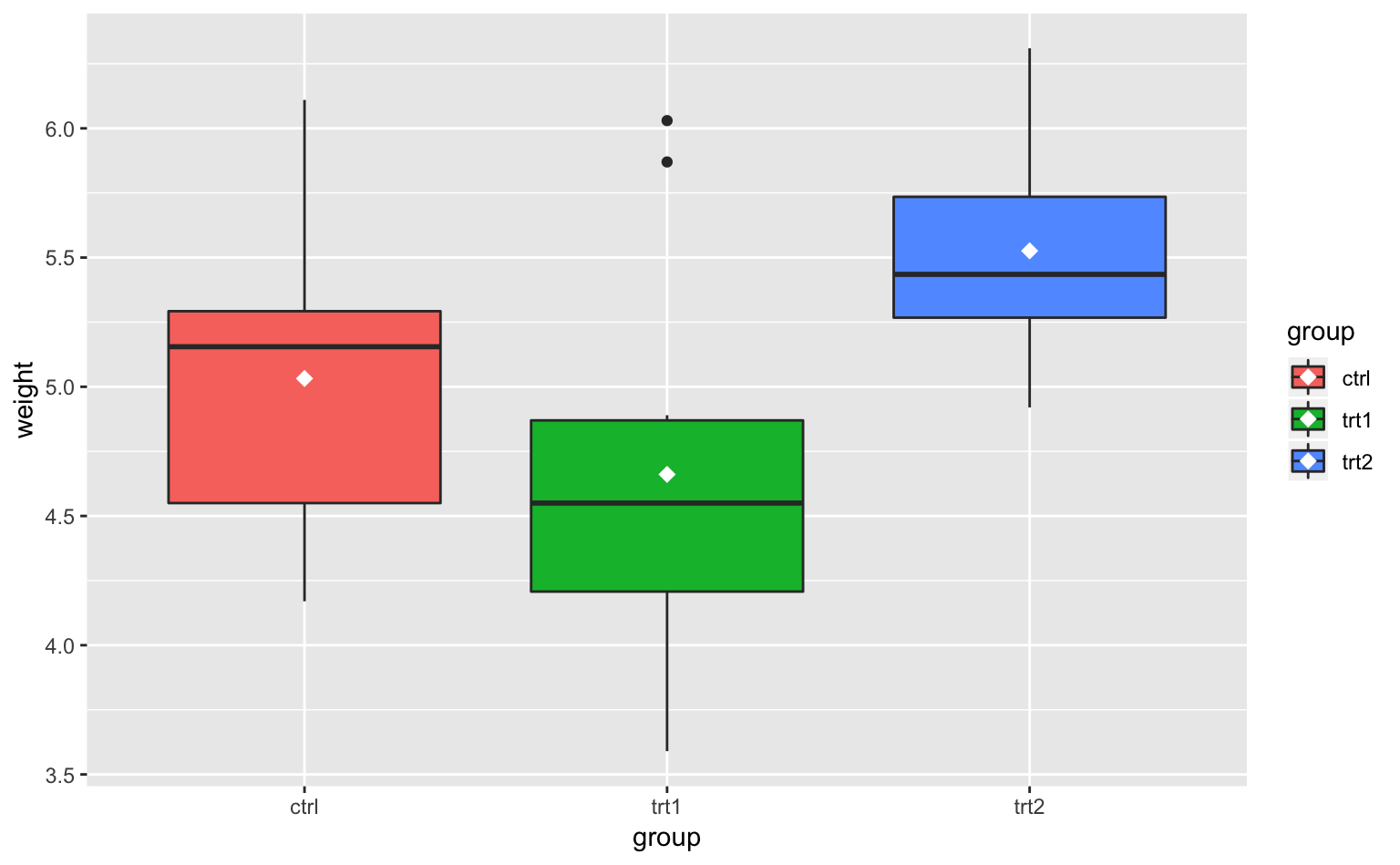

Figure 4.13: 平均値を追加した箱ひげ図。

stat_summary()は統計量をプロットするための関数である。このグラフでは「y（weight）の平均値をサイズ3の白いひし形で描いてください」と指示している。各引数の意味はなんとなくわかると思うので、説明は割愛する。

4.4 バイオリンプロット

箱ひげ図に似たものとして、バイオリンプロット（violin plot）がある。バイオリンプロットとは、密度プロットを90°回転させ、アジの干物のように開いたグラフである。

バイオリンプロットは、geom_violin()で描くことができる。

ggplot(PlantGrowth, aes(group, weight, fill = group)) + # x軸にgroup、y軸にweight、fillで塗りつぶし
  geom_violin() # バイオリンプロットを描くためのコード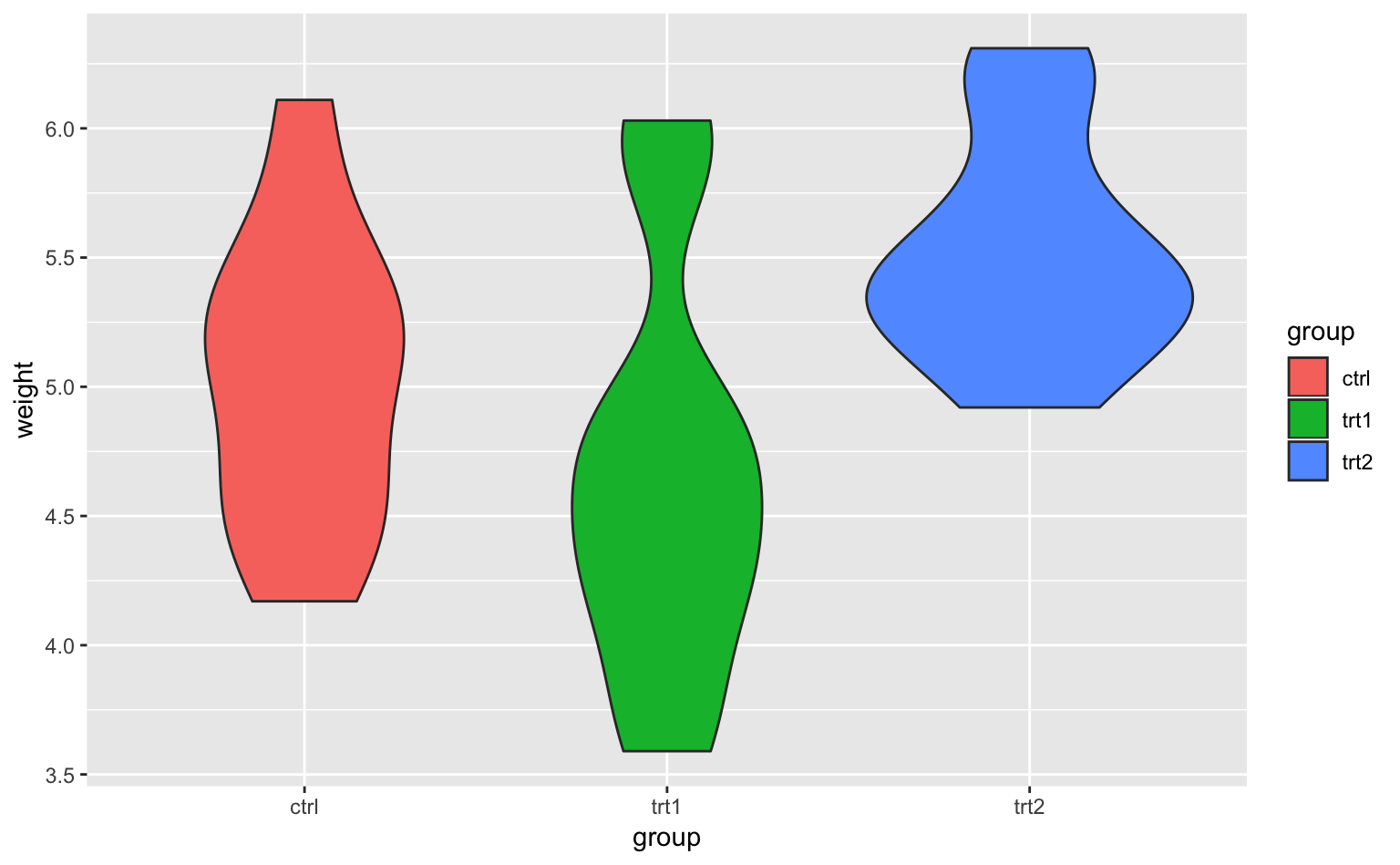

Figure 4.14: バイオリンプロット。x軸は条件、y軸は植物の重さを表している。

このように、バイオリンプロットを使うと、分布の形状が箱ひげ図よりも直観的にわかるようになる。なお、geom_density()と同様に、geom_violin()でも、カーネル密度推定用のパラメタ（adjust）をいじることができるので、いくつか試してみてほしい。

4.5 ストリッププロット

箱ひげ図／バイオリンプロットは、ストリッププロット（strip plot）とも相性が良い。ストリッププロットとは、1つ1つのデータをそのままドットとして表現したグラフである。この説明ではイメージが湧きにくいと思うので、とりあえず下のプロットを見てほしい。

ggplot(PlantGrowth, aes(group, weight, fill = group)) + # x軸にgroup、y軸にweight、fillで塗りつぶし
  geom_violin() + # まずバイオリンプロット
  geom_boxplot(outlier.shape = NA, width = 0.2) + # その上に箱ひげ図
  geom_point(position = position_jitter(width = 0.1, height = 0, seed = 1)) + # その上にストリッププロット
  stat_summary(geom = "point", fun.y = mean, shape = "diamond", color = "white", size = 3) # おまけに平均値を追加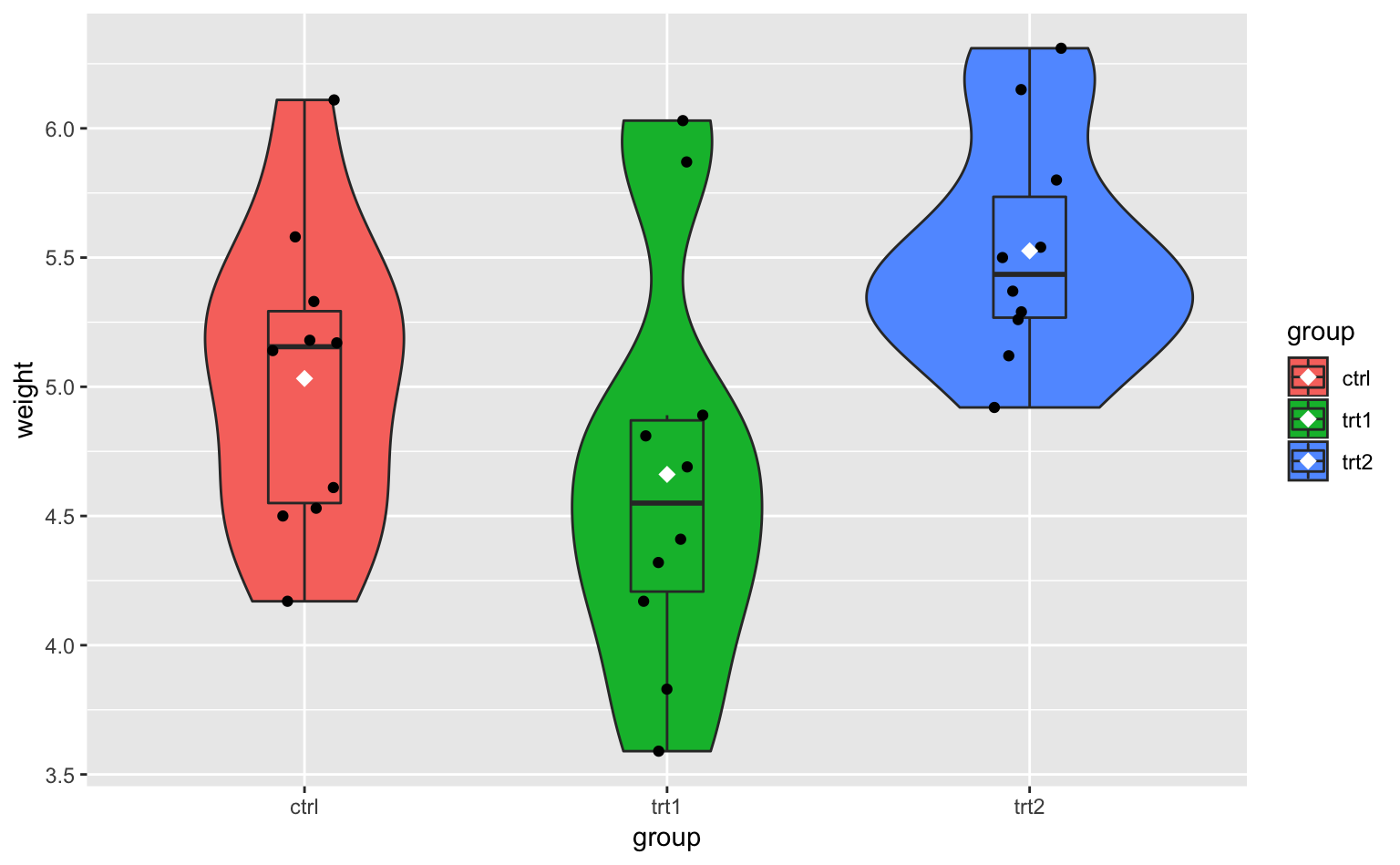

Figure 4.15: ストリッププロットを箱ひげ図とバイオリンプロットの上に重ね合わせた図。ドットはデータそのものを表している。

図中の黒いドットたちがストリッププロットである。1個1個のドットはデータそのものを表している。

コードの内容を上から順に解説する。

ggplot(PlantGrowth, aes(group, weight, fill = group))
- x軸にgroup、y軸にweightを指定。groupごとに塗りつぶす。
geom_violin()
- バイオリンプロットを描く。
geom_boxplot(outlier.shape = NA, width = 0.2)
- その上に箱ひげ図を描く。
- outlier.shape = NAとして外れ値を消すのがポイント。デフォルトだと、箱ひげ図の外れ値とストリッププロットのドットが混在してしまう。
- widthは箱ひげ図の幅を調整する引数。1がデフォルトの大きさ。
geom_point(position = position_jitter(width = 0.1, seed = 1))
- さらにストリッププロット（ドット）を描く。
- position = position_jitter()はドットの位置をジッター（jitter：散らばらせる）ための関数である。これを設定しないと、ドットが縦一列に並んでしまい、データ構造が非常に見づらくなる（気になる人は、試しにposition以下を消して実行してみよう）。
- widthは水平（x軸）方向の散らばり幅を調整する引数。また、seedはジッター具合を決めるための引数（乱数生成のシード）である。これを決めないと毎回ドットの位置が変わってしまうので、再現性を担保するためにも設定しておくと良い（気になる人は、試しにseed以下を消した上で何回か実行してみよう）。
- この図の場合、ドットが垂直（y軸）方向にも散らばっていると、誤解を招く結果を導きかねない。そのため、height（垂直方向の散らばりの大きさ）は0にしている。
stat_summary(geom = "point", fun.y = mean, shape = "diamond", color = "white", size = 3)
- おまけに平均値を描く。

データポイントがそこまで大量でない場合は、このようにプロットするのが良いだろう。

4.6 練習問題

Rにデフォルトで入っているiris（アヤメに関するデータセット¹³ ）を使い、SpeciesごとにSepal.Lengthのヒストグラムと密度プロットをそれぞれ描いてみよう。
SpeciesごとにSepal.Widthの箱ひげ図、バイオリンプロット、ストリッププロットを重ね書きしてみよう。

色々なスタイル・流派があるらしいが、ここでは最もよく使われるTukeyの箱ひげ図を説明している。↩
平均値は外れ値に引っ張られるので、分布の代表値としては中央値のほうが妥当な場合が多い。箱ひげ図がデフォルトで平均値を描かないのもおそらくはそのため。↩
様々なデータ分析においてチュートリアル的に用いられる代表的なデータセット。https://en.wikipedia.org/wiki/Iris_flower_data_set ↩