5 連続変数間の関係
連続変数間の関係を見たいときは、散布図(scatter plot)を描くのがセオリーである。
library(ggplot2) # 忘れずにパッケージを読み込む5.1 基本の散布図
ここでは、Rにデフォルトで入っているfaithful(オールド・フェイスフル・ガイザーに関するデータセット)を使ってみよう。ちなみに、オールド・フェイスフル・ガイザーとは、イエローストーン国立公園内にある間欠泉のことである14。
head(faithful) # 先頭6行## eruptions waiting
## 1 3.600 79
## 2 1.800 54
## 3 3.333 74
## 4 2.283 62
## 5 4.533 85
## 6 2.883 55変数はそれぞれ、
eruptions:間欠泉の噴出時間(分)waiting:次の間欠泉が噴出するまでの時間(分)
を表している。散布図はドットから構成されるグラフなので、geom_point()で描くことができる。
ggplot(faithful, aes(eruptions, waiting)) + # x軸にeruptions、y軸にwaiting
geom_point() # 散布図を描く(データをドットとして表示する)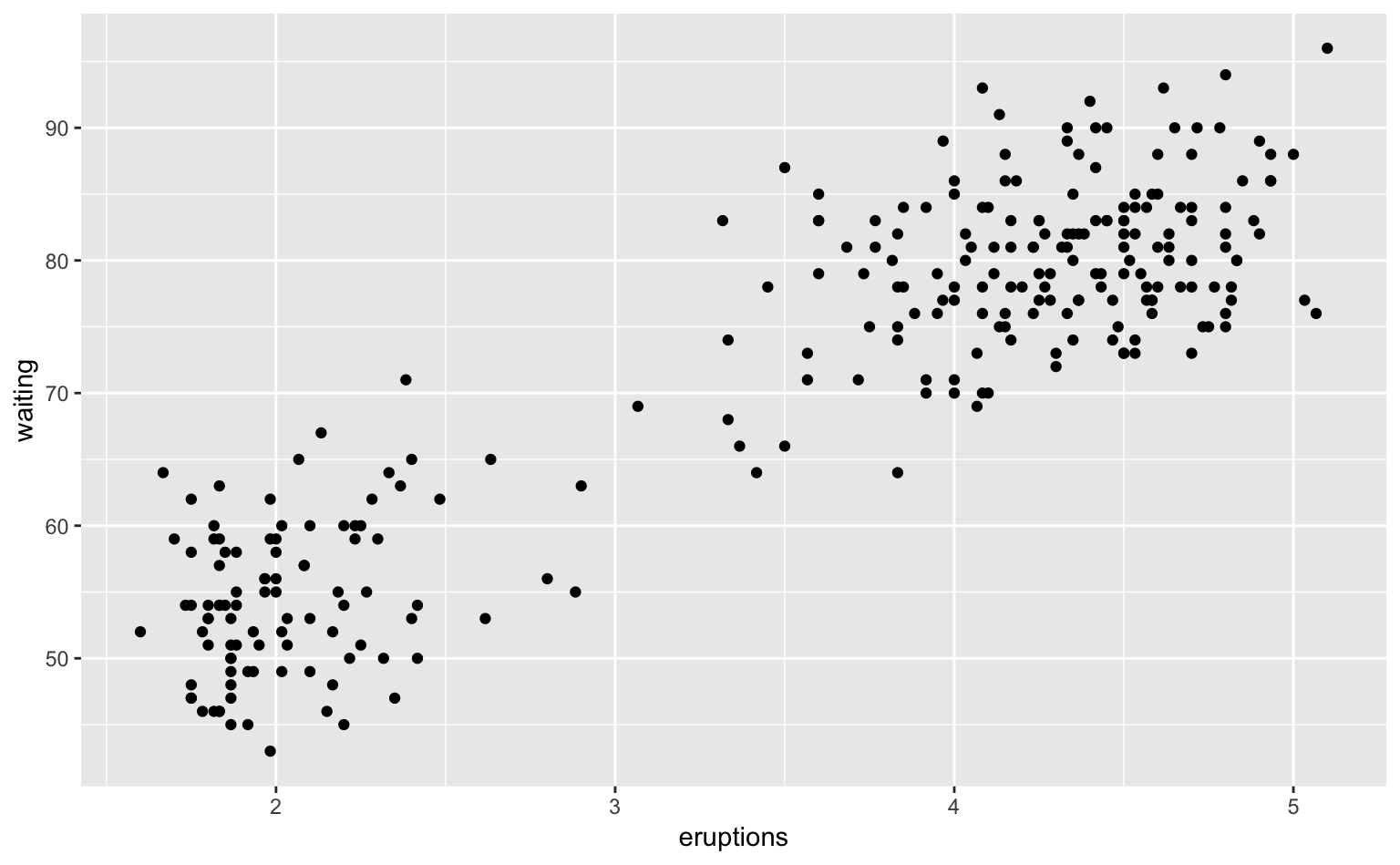
Figure 5.1: faithfulデータの散布図。強い正の相関が見て取れる。また、データを2つのクラスタに分けられそうなことが見て取れる。
5.2 グルーピングされた散布図
Chapter 2のチュートリアルでも見たが、複数グループの散布図を描く(グルーピングする)ことも可能である。Rにデフォルトで入っているmtcarsを使い、改めてChapter 2で描いた散布図の復習をしよう。geom_point()でグループごとに色を変えるには、colorに変数を指定すれば良い。
ggplot(mtcars, aes(wt, mpg, color = factor(cyl))) + # factor(変数)とすることで、離散変数として扱える
geom_point()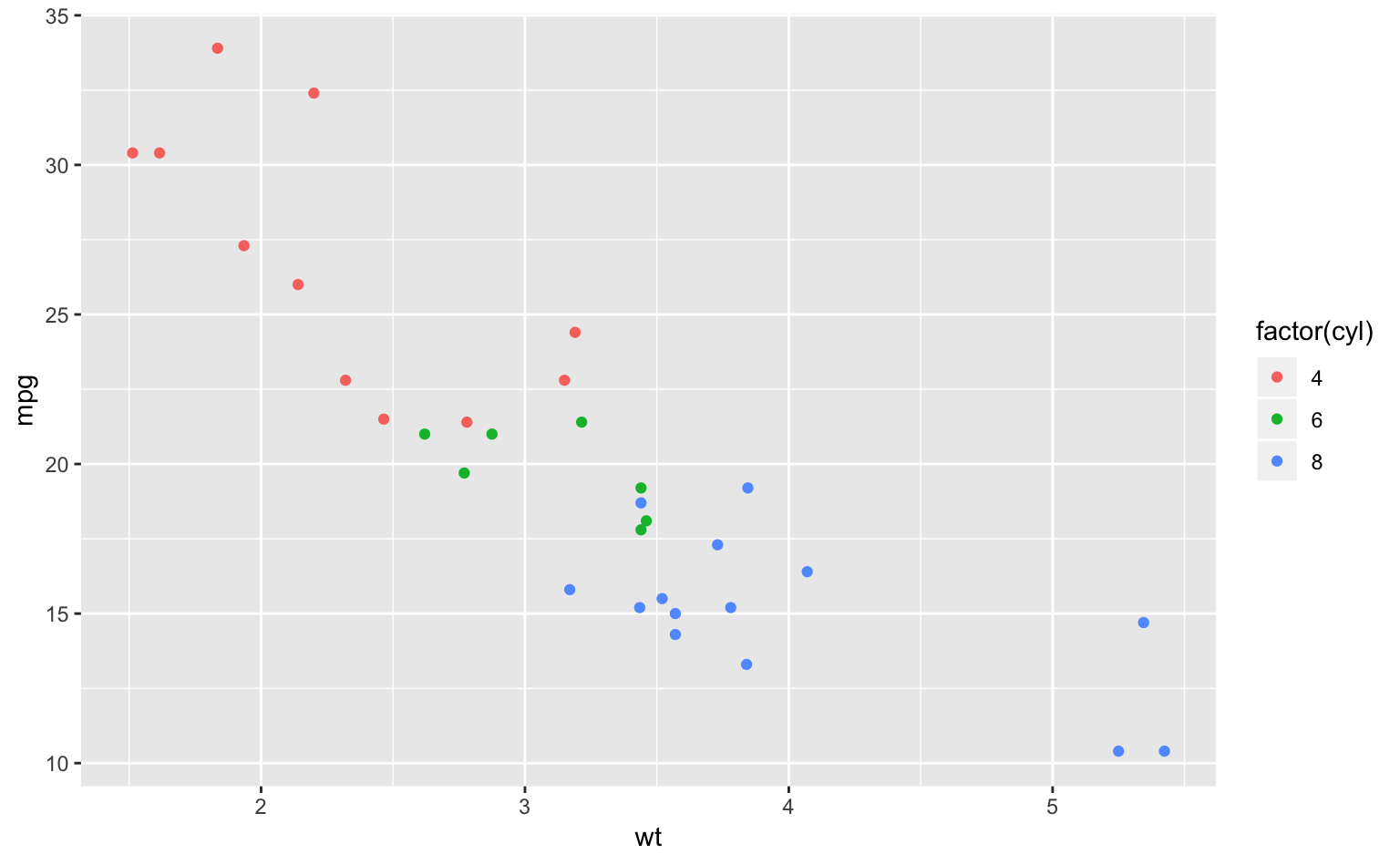
Figure 5.2: グルーピングされた散布図。
見やすさや色覚バリアフリーという観点に立てば、点の形も変えたほうが良いだろう15。ドットの形を変えるには、shapeに変数を指定すれば良い。
ggplot(mtcars, aes(disp, mpg, color = factor(cyl), shape = factor(cyl))) + # shape = factor(cyl)を追加
geom_point()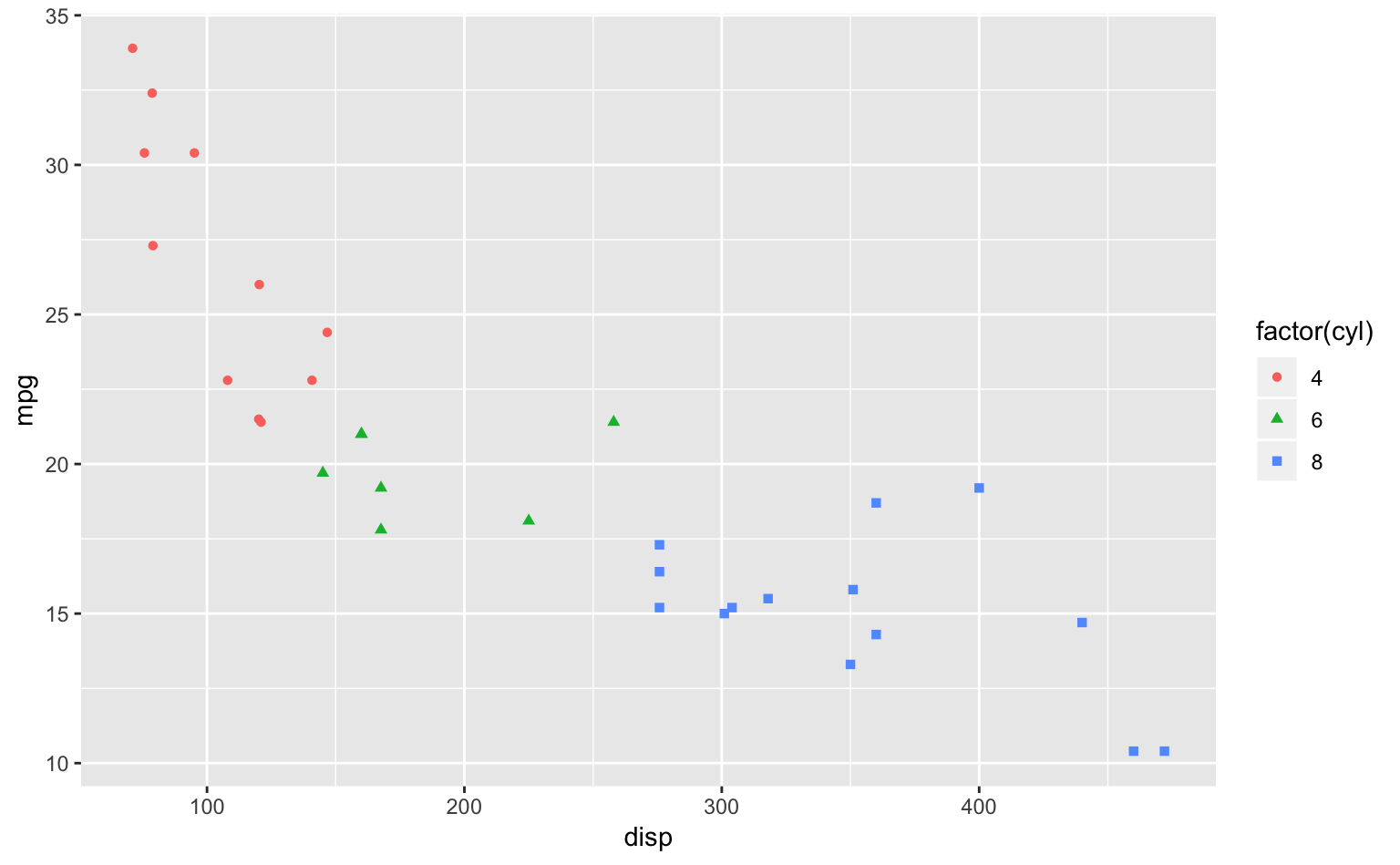
Figure 5.3: Figure 5.2のドットの形を変えた散布図。
cyl(シリンダーの個数)の値に応じてデータポイントの形が変わっているのが見て取れる。
5.3 散布図行列
faithfulデータは変数が2つだけなので、散布図を1つ描けば終わりである。しかし、実際のデータには多くの変数がある。変数が増えるにつれて、確認しなければならない散布図の数は爆発的に増える。そのようなとき、1つ1つ散布図を描くのは面倒である。
しかし、そんなときに便利なものがある16。それは、GGallyパッケージのggpairs()という関数である。では早速、Rにデフォルトで入っているirisデータで試してみよう。まずはGGallyパッケージを読み込む。
library(GGally) # パッケージの読み込みあとは、ggpairs()にデータセットを突っ込むだけ。以上。
ggpairs(iris) # 散布図行列を描く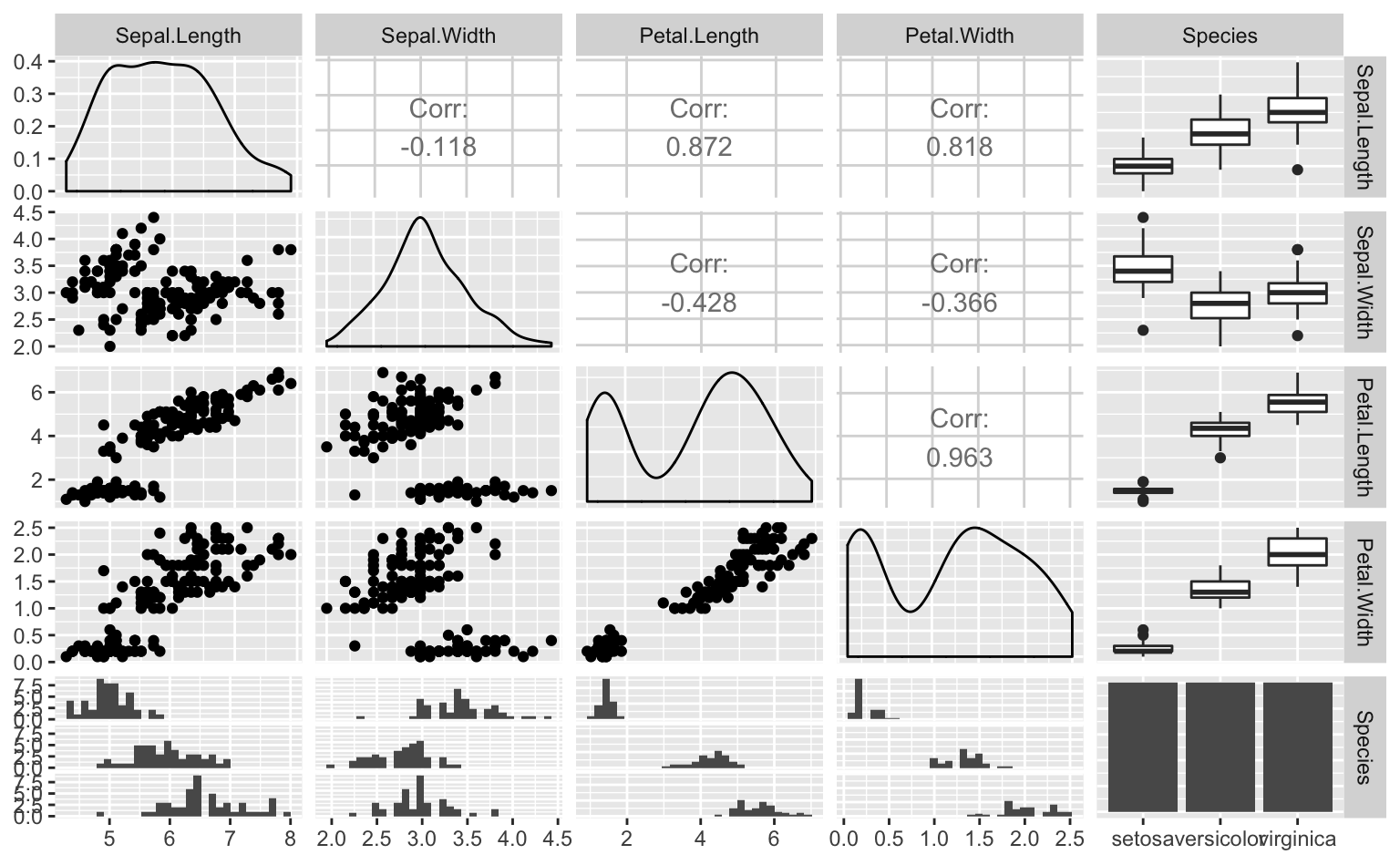
Figure 5.4: ggpairs()によるirisデータの散布図行列。散布図だけでなく、変数の種類に応じて自動で箱ひげ図などもプロットされる。
なんと、これだけで多変量の散布図、箱ひげ図などを一撃で描画できてしまうのである。しかも、変数の連続/離散に応じて適切なグラフを選んでくれる親切ゆとり設計である。
ただ、これだけでは少し味気ないので、Speciesに応じて色をつけてみよう。ggplot2と同じように指定すれば良い。
ggpairs(iris, aes(color = Species, alpha = 0.7)) # ggplot2と同じように色と透明度を指定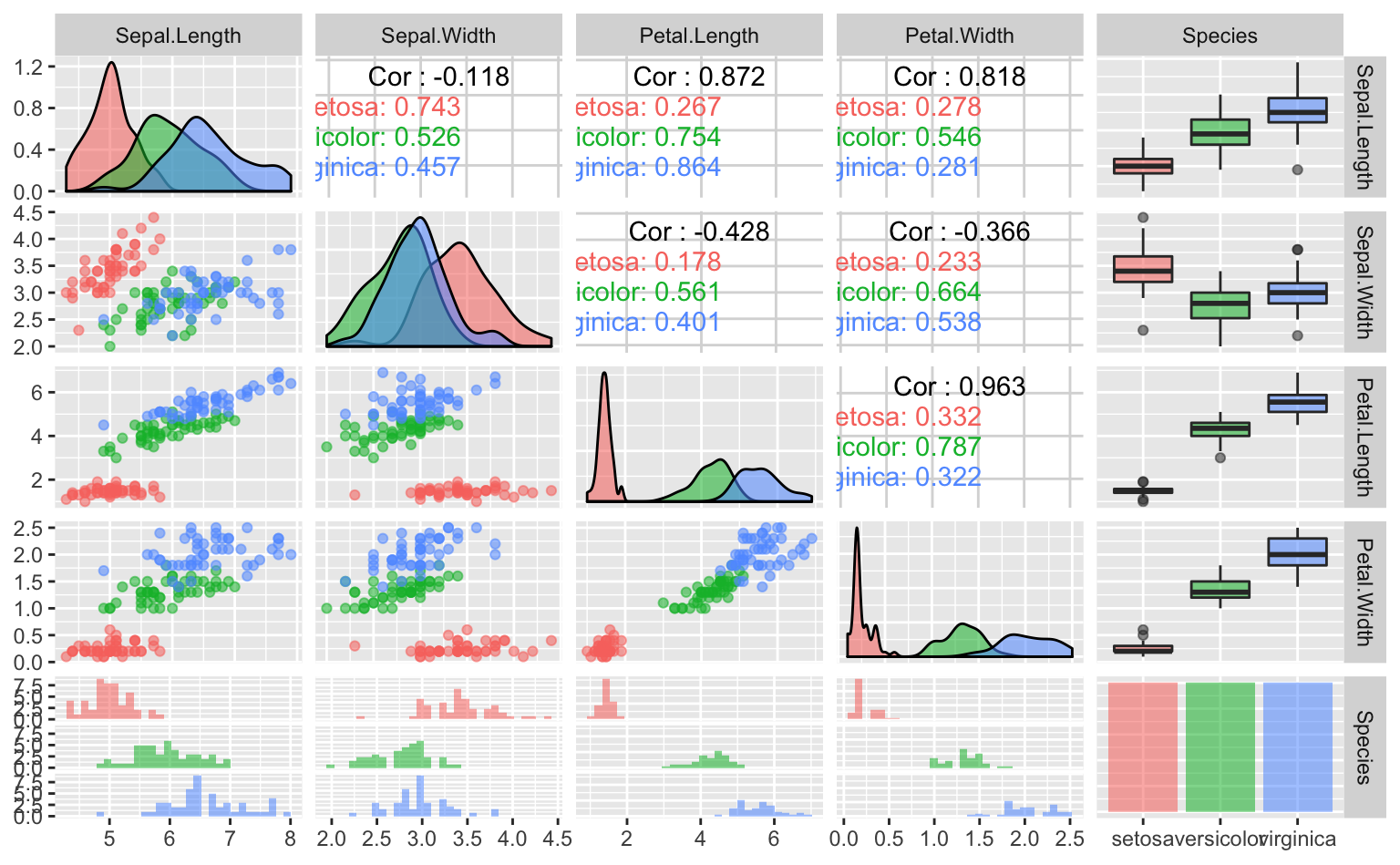
Figure 5.5: Figure 5.4に色をつけて半透明にした図。
他にも細かい設定ができるそうだが、ここでは説明を割愛する17。
5.4 オーバープロットへの対処
最後に、オーバープロットというものへの対処法を見ていくことにする。具体例として、ggplot2に入っているmpgデータを使ってみよう。
head(mpg) # 先頭6行## # A tibble: 6 x 11
## manufacturer model displ year cyl trans drv cty hwy fl
## <chr> <chr> <dbl> <int> <int> <chr> <chr> <int> <int> <chr>
## 1 audi a4 1.8 1999 4 auto(l5) f 18 29 p
## 2 audi a4 1.8 1999 4 manual(m5) f 21 29 p
## 3 audi a4 2 2008 4 manual(m6) f 20 31 p
## 4 audi a4 2 2008 4 auto(av) f 21 30 p
## 5 audi a4 2.8 1999 6 auto(l5) f 16 26 p
## 6 audi a4 2.8 1999 6 manual(m5) f 18 26 p
## class
## <chr>
## 1 compact
## 2 compact
## 3 compact
## 4 compact
## 5 compact
## 6 compact注目する変数は、
displ:エンジンの排気量(リットル)hwy:燃費(マイル/ガロン)cyl:シリンダー数(4, 5, 6, or 8)
の3つである。早速、xにdispl、yにhwy、colorにfactor(cyl)を指定して散布図を描いてみよう。
ggplot(mpg, aes(displ, hwy, color = factor(cyl))) +
geom_point()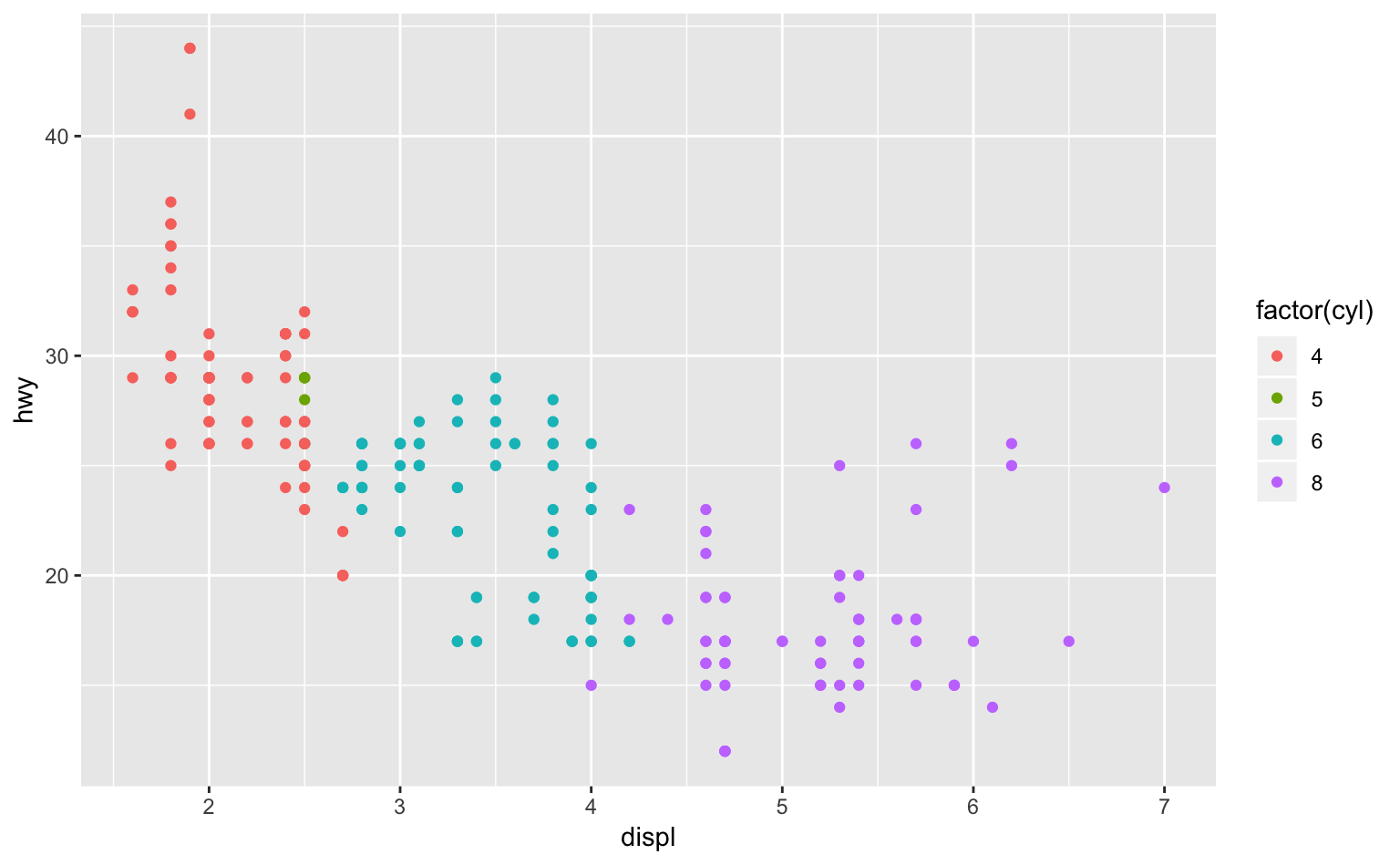
Figure 5.6: デフォルトの設定で描いた散布図。
とりあえず散布図を描くことができた。一見問題は無さそうである。
では、ここでmpgのデータの行数(データポイントの数)を確認してみよう。nrow(データセット)で確認することができる。
nrow(mpg)## [1] 234なんと234個もあった。しかし、Figure 5.6の散布図では、データ(ドット)がせいぜい数十〜百個ぐらいにしか見えない。なぜだろうか?
なぜなら、x軸の値とy軸の値が全く同じデータポイントが複数個存在しており、それらが重なってしまっているからである。このような状態をオーバープロット(overplotting)という。
たとえば、7件法のリカート尺度によって実験参加者の特性を測り、その散布図を描くというときに、オーバープロットは間違いなく生じる。では、どのように対処すればよいのだろうか? ここでは、Chapter 4でも扱ったジッター(jittering)というテクニックを使えば良い。
ggplot(mpg, aes(displ, hwy, color = factor(cyl))) +
geom_point(position = position_jitter(width = 0.1, height = 0.4, seed = 1)) # ドットをジッターさせている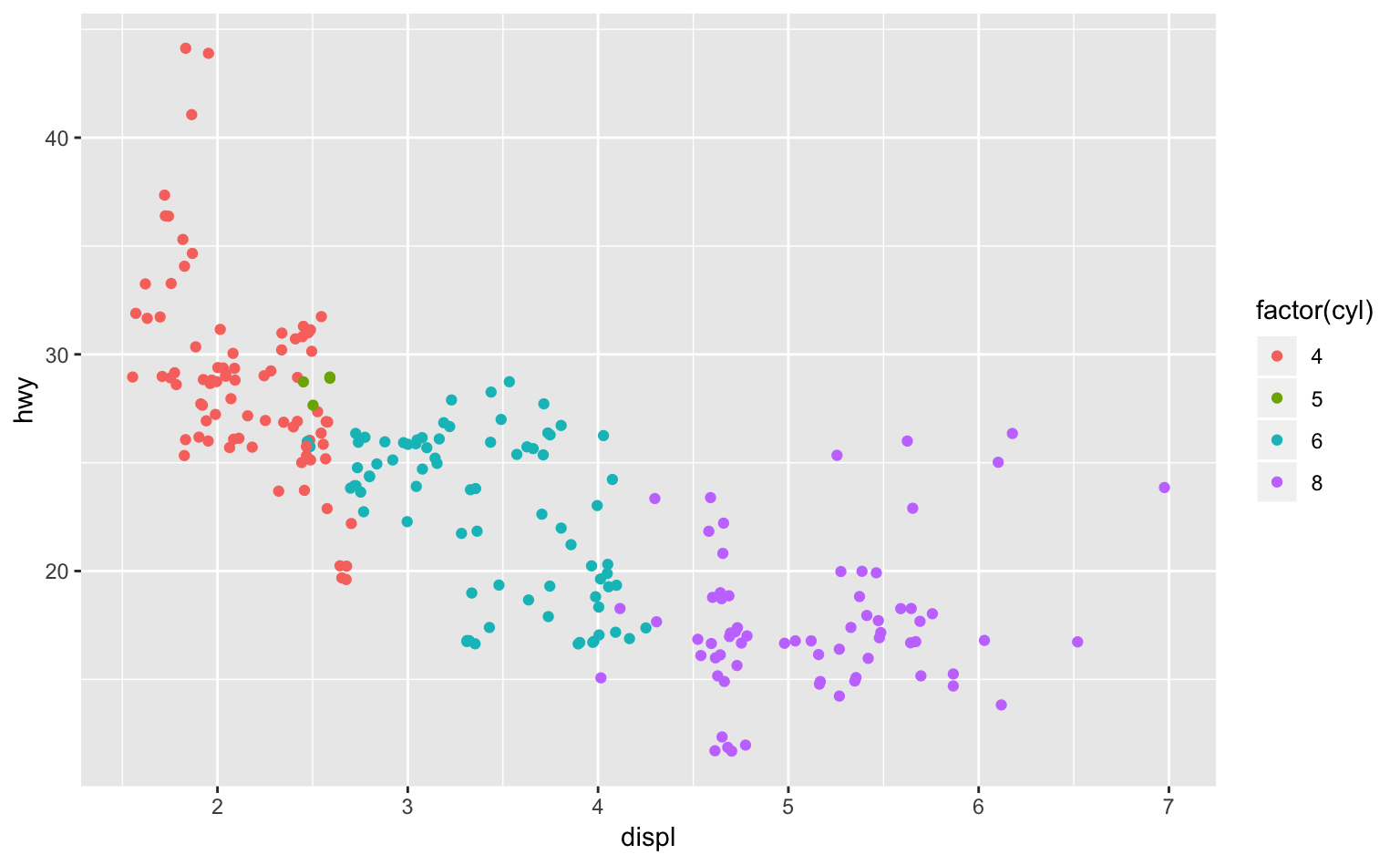
Figure 5.7: ドットをジッターさせた散布図。
position = position_jitter(width = ..., height = ..., seed = ...)を指定することで、オーバープロットを回避することができた。このとき、widthやheightに大きすぎる値を入れてしまうと、データが大きく歪んでしまうので注意が必要である。
また、ここで点の形状や透明度を調節すれば、重複している箇所がより見やすくなって良いだろう。
ggplot(mpg, aes(displ, hwy, color = factor(cyl), shape = factor(cyl))) + # shapeに変数を指定
geom_point(position = position_jitter(width = 0.1, height = 0.4, seed = 1), alpha = 0.7) # alpha = 0.7を追加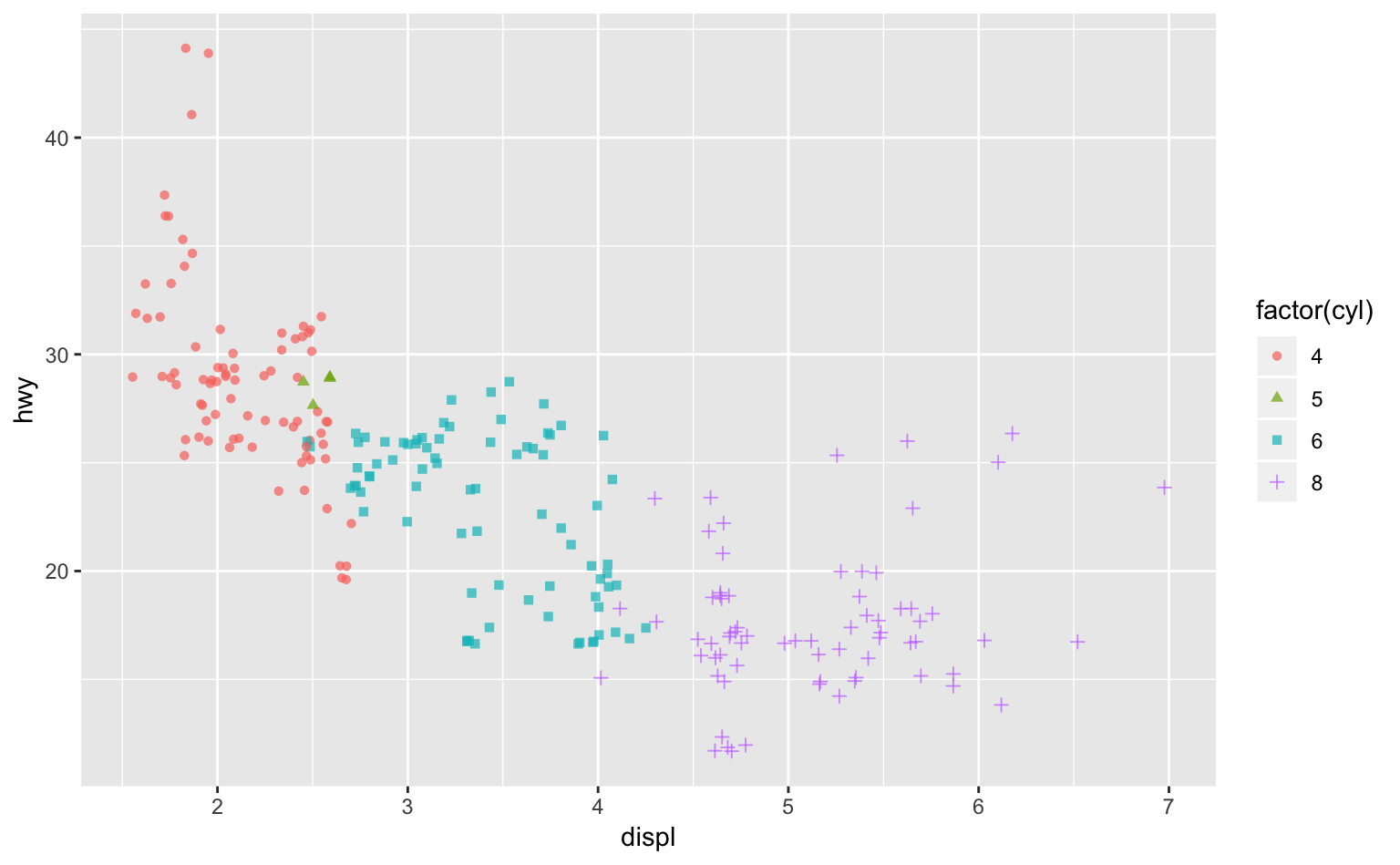
Figure 5.8: Figure 5.7のドットの形状と透明度を変えたもの。
5.5 練習問題
Rにデフォルトで入っている
treesデータを使い、GirthとVolumeの散布図を描いてみよう。gcookbookの
heightweightデータの散布図行列を描いてみよう。